Классическое и геометрическое определения вероятности
В практической деятельности часто приходится сталкиваться со случайными событиями, т.е. с событиями, которые могут произойти, но могут и не произойти по причинам, не поддающимся непосредственному учету в данных условиях. Изучение количественных закономерностей, которым подчиняются массовые однородные случайные события, и составляет предмет теории вероятностей.
При классическом определении вероятность события определяется равенством:
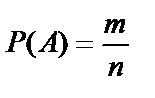 , (10.8)
, (10.8)
где m – число элементарных исходов испытания, благоприятствующих появлению события A; n – общее число произведенных испытаний.
Одним из недостатков классического определения вероятности, ограничивающим его применение, является то, что оно предполагает конечное число возможных исходов испытания.
Этот недостаток можно преодолеть, используя геометрическое определение вероятности, т.е. находя вероятность попадания точки в некоторую область (отрезок, часть плоскости и т.п.).
Геометрической вероятностью события A называется отношение меры области, благоприятствующей появлению события A, к мере всей области, т.е.
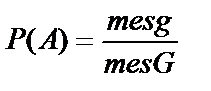 . (10.9)
. (10.9)
Пример 1. Найти вероятность того, что получится слово «ананас», если на отдельных карточках написаны три буквы «А», две буквы «Н» и одна буква «С».
Решение.
А – получится слово «АНАНАС».
Общее число случаев равно числу перестановок с повторениями из шести элементов, т.е. 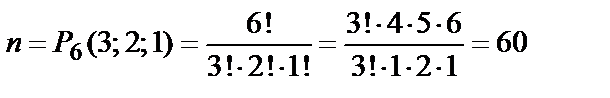 , из которых событию A благоприятствует одна комбинация m = 1. Искомая вероятность
, из которых событию A благоприятствует одна комбинация m = 1. Искомая вероятность
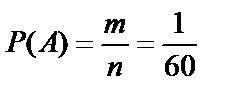 .
.
Пример 2. Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 7.
Решение.
А–сумма выпавших очков равна 7.
При бросании одной игральной кости возможны 6 элементарных исходов (1, 2, 3, 4, 5 и 6 очков), каждый из которых может сочетаться с 6-ю исходами на второй кости. Следовательно, общее число элементарных исходов равно n = 6·6 = 36.
Благоприятствующими являются следующие элементарные исходы: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1, т.е. их число равно m = 6.
Согласно классическому определению вероятности, получаем:
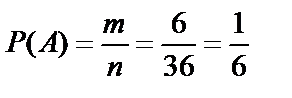 .
.
Пример 3. В бригаде работают 6 мужчин и 4 женщины. Среди членов бригады разыгрываются 7 билетов в театр. Найти вероятность того, что среди обладателей билетов окажутся 3 женщины.
Решение.
А– среди обладателей 7 билетов окажутся 3 женщины.
Общее число возможных элементарных исходов равно числу сочетаний из 10 элементов по 7 элементов, т.е.
 .
.
Подсчитаем число благоприятствующих исходов. 3 женщин из 4 можно отобрать 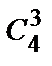 способами, оставшихся 4 человек из 6-ти можно отобрать
способами, оставшихся 4 человек из 6-ти можно отобрать 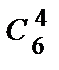 способами. Следовательно,
способами. Следовательно,
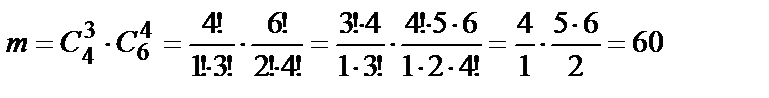 .
.
Искомая вероятность равна:
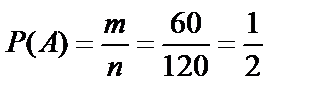 .
.
Пример 4.Буквы Т, Е, И, Я, Р, О написаны на отдельных карточках. Ребенок берет карточки в случайном порядке и прикладывает одну к другой: а) 3 карточки; б) все 6 карточек. Какова вероятность того, что получится слово: а) «ТОР»; б) «ТЕОРИЯ»?
Решение.
а) А–получение слова «ТОР».
Различные комбинации трех букв из имеющихся шести представляют размещения, т.к. могут отличаться как составом входящих букв, так и порядком их следования, то есть общее число случаев 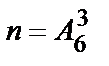 , из которых благоприятствуют событию A m = 1 случай.
, из которых благоприятствуют событию A m = 1 случай.
Получаем:
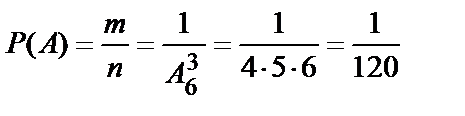 .
.
б) В– получение слова «ТЕОРИЯ».
Различные комбинации шести букв из имеющихся шести представляют собой перестановки, т.к. отличаются только порядком следования букв; т.е. общее число случаев 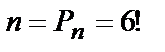 , из которых благоприятствуют событию B m = 1 случай. Поэтому
, из которых благоприятствуют событию B m = 1 случай. Поэтому
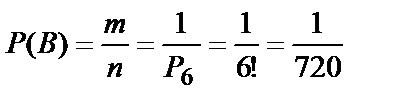 .
.
Пример 5. На отрезок единичной длины наудачу поставлена точка. Определить вероятность того, что расстояние от точки до концов отрезка превосходит величину 1/3.
Решение.
Пусть А –расстояние от точки до концов отрезка превосходит величину 1/3.
Построим отрезок OA единичной длины и разобьем его точками C и D таким образом, чтобы │OC│=1/3 и │DA│=1/3.
├−−−−┼−−−−┼−−−−┤
O C D A
Требование задачи будет выполнено, если точка попадет на отрезок CD длины 1/3. Тогда, согласно геометрической вероятности, искомая вероятность вычисляется по формуле:
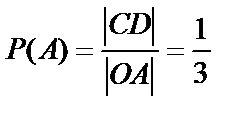 .
.
Дата добавления: 2018-11-26; просмотров: 2910;











