Теорема сложения вероятностей (для несовместных событий).
Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Р(А+В)=Р(А)+Р(В). (10.10)
Следствие 1.Сумма вероятностей событий, образующих полную группу, равна единице:
.
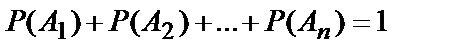Следствие 2.Сумма вероятностей противоположных событий равна единице:
.
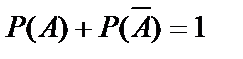Теорема сложения(для совместных событий).
Вероятность того, что наступит одно из совместных событий, равна сумме вероятностей этих событий, из которой вычтена вероятность общего наступления обоих событий, то есть произведение вероятностей.
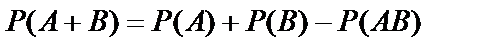. (10.11)
Теорема умножения вероятностей(для независимых событий).
Вероятность совместного появления двух независимых событий равна вероятностей этих событий:
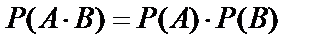. (10.12)
Следствие. Вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий:
.
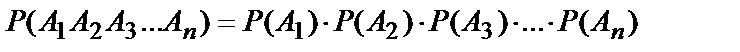Теорема умножения(для зависимых событий).
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже произошло:
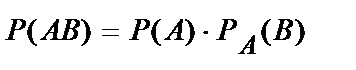. (10.13)
Следствие. Вероятность произведения нескольких событий равна произведению вероятности одного из этих событий на условные вероятности других; при этом условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли:
.
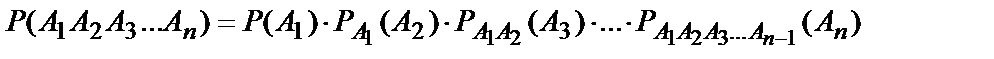Теорема(вероятность появления хотя бы одного события).
Вероятность появления хотя бы одного из событий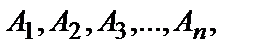 
независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий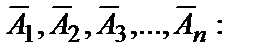 
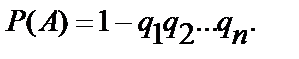
Частный случай. Если события 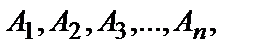имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий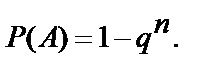 
Пример 1. Вероятность того, что будет снег (событие A), равна 0,6, а того, что будет дождь (событие B), равна 0,5. Найти вероятность плохой погоды, если вероятность дождя со снегом (событие AB) равна 0,25.
Решение.
События A и B совместны, поэтому
P(A+B) = P(A) + P(B) − P(AB) = 0,6 + 0,45−0,25 = 0,8
Пример 2.В денежно – вещевой лотерее на каждые 10 000 билетов разыгрывается 150 вещевых и 50 денежных выигрышей. Чему равна вероятность выигрыша, безразлично денежного или вещевого, для владельца одного лотерейного билета?
Решение.
A–выигрыш одного билета;
A1 – вещевой выигрыш;
A2 – денежный выигрыш.
, 
.
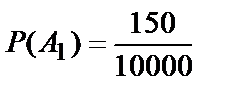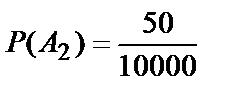По теореме сложения имеем:
.
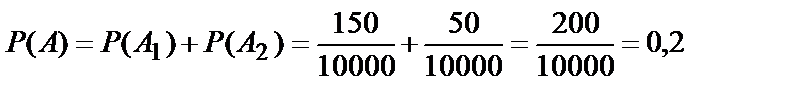Пример 3.Бросают две игральные кости. Какова вероятность того, что сумма выпавших очков равна 12?
Решение.
A –сумма выпавших очков равна 12;
A1 – 6 очков на первой кости;
A2 –6 очков на второй кости.
.
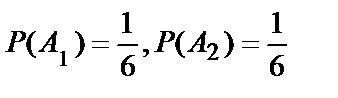По теореме умножения независимых событий:
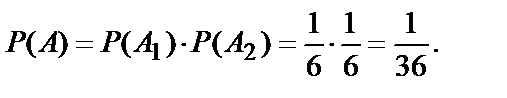
Пример 4.В урне 20 белых и 6 черных шаров. Из нее вынимают два шара. Найти вероятность того, что оба шара черные.
Решение.
A–оба шара черные;
A1 – 1-й шар черный;
A2 – 2-й шар черный.
.
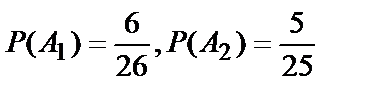По теореме умножения:
.
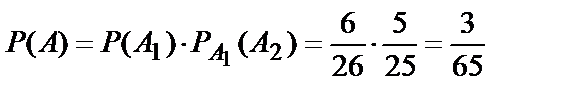Пример 5. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1=0,8; p2=0,7; p3=0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.
Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события A1 (попадание первого орудия), A2 (попадание второго орудия) и A3 (попадание третьего орудия) независимы в совокупности. Вероятности событий, противоположных событиям A1, A2 и А3(т.е. вероятности промахов), соответственно равны:
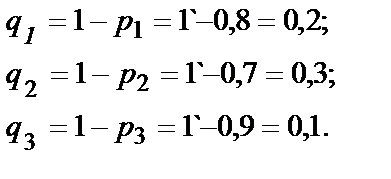
Искомая вероятность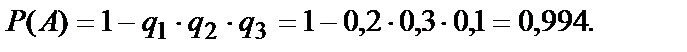 
Дата добавления: 2018-11-26; просмотров: 1113;
Поиск по сайту
Узнать еще
- C) Теорема затухания (Теорема смещения)
- II закон термодинамики. Теорема Карно-Клаузиуса
- II. Аксиомы вероятностей
- Аксиоматический подход к теории вероятностей
- Аксиоматическое построение теории вероятностей
- Биномиальное распределение и измерение вероятностей
- В теории вероятностей и её приложениях нормальное распределение играет особо важную роль.
- Виды гимнастики, направленные по преимуществу на формирование телосложения и улучшение состава тела
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
