ТЕОРИЯ Вероятностей

Теория вероятностей –математическая наука, изучающая закономерности случайных явлений. Под случайными явлениями понимаются явления с неопределенным исходом, происходящие при неоднократном воспроизведении определенного комплекса условий.

10.1 Элементы комбинаторики

Факториалом натурального числа n называется число

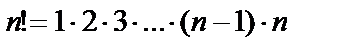. (10.1)

По определению, факториалом нуля является единица:

0!=1.

Рассмотрим некоторое множество S , состоящее из n различных элементов. Пусть 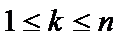. Назовём множество, состоящее из k элементов, упорядоченным, если каждому элементу этого множества поставлено в соответствие число от 1 до k , причём различным элементам множества соответствуют разные числа.

Размещениями из n элементов по kназываются упорядоченные подмножества множества S,состоящие из k различных элементов и отличающиеся друг от друга составом элементов или порядком их расположения.

Число размещений из n элементов по k равно

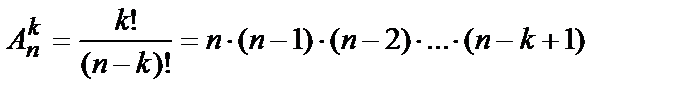. (10.2)

Перестановками из n элементовназываются размещения из n элементов по n,т. е. упорядоченные подмножества множества S, состоящие из всех элементов данного множества и отличающиеся друг от друга только порядком их расположения.

Число перестановок из n элементов равно

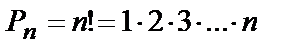. (10.3)

Сочетаниями из n элементов по kназываются подмножества множества S , состоящие из k различных элементов и отличающиеся друг от друга только составом элементов.

Число сочетаний из n элементов по k равно

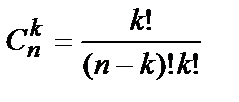. (10.4)

Размещениями с повторениями из n элементов по k называются упорядоченные подмножества множества S , состоящие из k элементов, среди которых могут оказаться одинаковые, и отличающиеся друг от друга составом элементов или порядком их расположения.

Число размещений с повторениями из n элементов по k равно

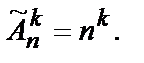(10.5)

Сочетаниями с повторениями из n элементов по kназываются подмножества множества S,состоящие из k элементов, среди которых могут оказаться одинаковые, и отличающиеся друг от друга только составом элементов.

Число сочетаний с повторениями из n элементов по k равно

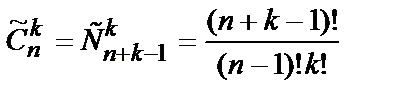. (10.6)

Если во множестве S, состоящем из n элементов, есть только m различных элементов, то перестановками с повторениями из n элементовназываются упорядоченные подмножества множества S , в которые первый элемент множества S входит n₁ раз, второй элемент — n₂ раз и так до

m -го элемента, который входит n_m раз (n₁ +n₂+…+n_m = n).

Число перестановок с повторениями из n элементов, в которые первый элемент множества S входит n₁ раз, второй элемент — n₂ раз и так до m -го элемента, который входит n_m раз(n₁ +n₂ +…+n_m = n), равно

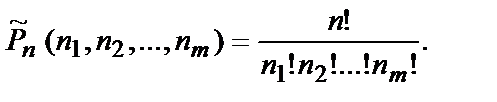(10.7)