Формула Бернулли. Приближенные формулы в схеме Бернулли

Формула Бернуллии. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0<p<1), событие наступит ровно k раз (безразлично в какой последовательности), равна:

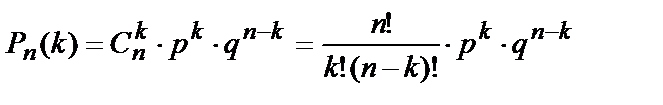, (10.16)

где q=1-p.

Вероятность того, что в n испытаниях событие наступит: а) менее k раз; б) более k раз; в) не менее k раз; г) не более k раз – находят соответственно по формулам:

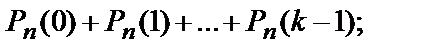
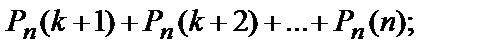
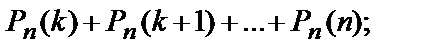
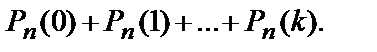
Наиболее вероятное число успехов в n испытаниях Бернулли удовлетворяет неравенству:

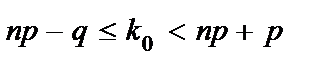, (10.17)

причем:

а) если число np – q – дробное, то существует одно наивероятнейшее число k₀;

б) если число np – q – целое, то существует два наивероятнейших числа, а именно k₀. и k₀ + 1;

в) если число np – целое, то наивероятнейшее число k₀.= np.

Формула Пуассона.Если число испытаний n велико, а вероятность p появления события в каждом испытании очень мала, то используют приближенную формулу Пуассона:

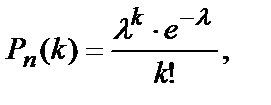(10.18)

где k – число появлений события в n независимых испытаниях, 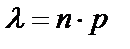– среднее число появлений события в n испытаниях.

Локальная теорема Муавра – Лапласа.Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0 < p < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)

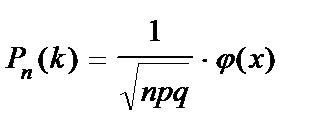, (10.19)

где .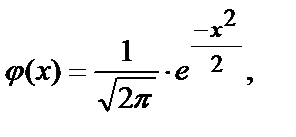

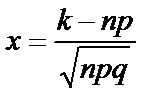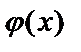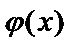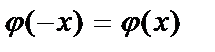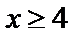Значения функции , соответствующие положительным значениям аргумента x, находят по таблицам. Для отрицательных значений аргумента пользуются теми же таблицами, так как функция четна, т.е. . При можно считать, что 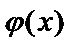=0.

Интегральная теорема Муавра – Лапласа.Вероятность того, что в n испытаниях, в каждом из которых вероятность появления события равна p (0 < p < 1), событие наступит не менее 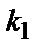раз и не более 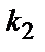раз, приближенно равна

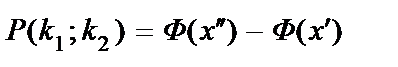, (10.20)

где 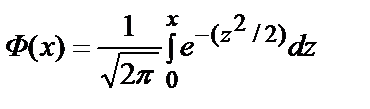– функция Лапласа, .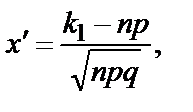

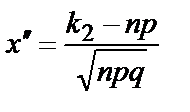Значения функции Лапласа для положительных значений x (0<x<5) приведены в таблице.

Для значений 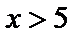полагают 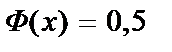. Для отрицательных значений x используют эту же таблицу, учитывая, что функция Лапласа нечетная:

.

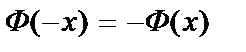10.6 Решение типовых примеров

Пример 1.Вероятность того, что в данный день торговая база уложится в норму расходов на транспорт, равна 3/4. Какова вероятность того, что лишь в один из дней рабочей недели (6 дней) база уложится в норму?

Решение.

A – база уложится в норму в один день из шести.

n = 6, k = 1, p = 3/4, q = 1/4.

Искомая вероятность по формуле Бернулли равна:

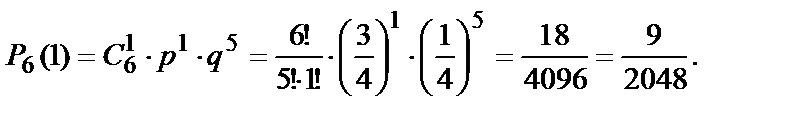
Пример 2.Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти вероятность появления не более 2-х бракованных деталей среди 5 отобранных.

Решение.

A – появление не более 2-х бракованных деталей среди 5 отобранных.

Вероятность изготовления бракованной детали .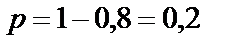

Искомая вероятность равна:

.

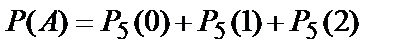Вычислим вероятности:

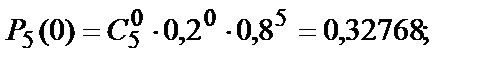
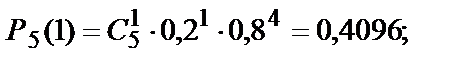
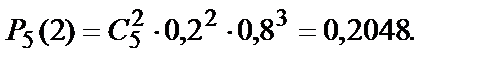
Получаем:

.

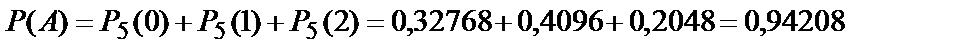Пример 3. Испытывается каждый из 15 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0,9. Найти наивероятнейшее число элементов, которые выдержат испытание.

Решение.

По условию, n=15, p=0,9, q=0,1. Найдем наивероятнейшее число k₀. из неравенства

.

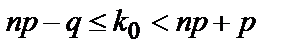Подставив данные задачи, получим

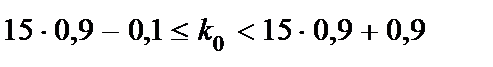или .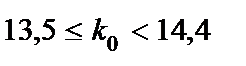

Так как np–q – дробное, то существует одно наивероятнейшее число k₀. Поскольку между числами 13,5 и 14,4 заключено одно целое число, а именно 14, то искомое наивероятнейшее число k₀.= 14.

Пример 4.На контрольно – семенную станцию поступило 200 семян сосны для определения всхожести. Вероятность того, что семя не взойдет, равна 0,01. Найти вероятность того, что среди 200 семян 6 не взойдёт.

Решение.

Так как число n велико, а вероятность p мала, то применим формулу Пуассона:

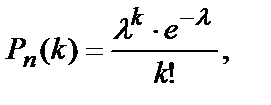где .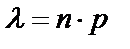

По условию .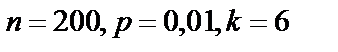

Вычислим .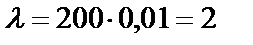

Искомая вероятность равна:

.

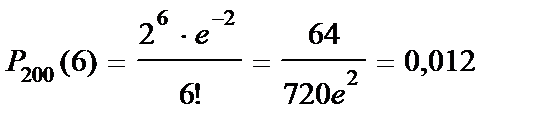Пример 5.Вероятность попадания в цель при одном выстреле равна 0,6. Найти вероятность того, что при 5400 выстрелах цель будет поражена 3240 раз.

Решение.

По условию задачи n=5400, p=0,6, q=0,4, k=3240. Воспользуемся локальной теоремой Муавра–Лапласа (10.19):

.

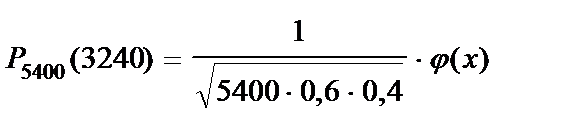Вычислим .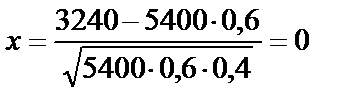

По таблице значений функции 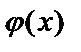находим: 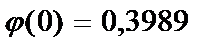, тогда искомая вероятность равна:

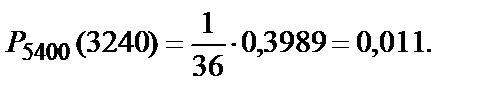
Пример 6.В некоторой местности из каждых 100 семей 80 имеют холодильники. Найти вероятность того, что от 300 до 360 (включительно) семей из 400 имеют холодильники.

Решение.

Вероятность того, что семья имеет холодильник, равна p = 80/100 = 0,8; 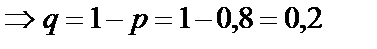– вероятность того, что семья не имеет холодильник.

По условию .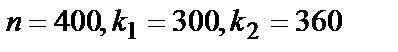

Воспользуемся интегральной теоремой Муавра – Лапласа (10.20):

.

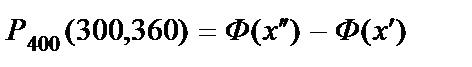Вычислим , .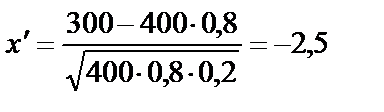

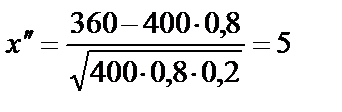Учитывая, что функция Лапласа нечетная, т.е. 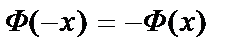, по таблице значений функции Ф(х) находим: .

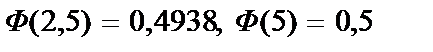Тогда искомая вероятность равна:

.

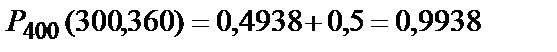Случайные величины

Случайнойназывают величину, которая в результате испытания примет одно и только одно возможное значение, наперёд не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Случайные величины обычно обозначают последними заглавными буквами латинского алфавита: X, Y, Z, а их возможные значения –соответствующими строчными буквами: x, y, z. Если случайная величина X имеет три возможных значения, то они будут обозначены: x₁, x₂, x₃.

Случайные величины задают законами распределения. Законы распределения могут быть заданы тремя способами: табличным, графическим, аналитическим. Способ задания зависит от типа случайной величины.

Случайные величины делятся на дискретные (прерывные) и непрерывные.

Дискретной(прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Непрерывнойназывают случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно.