Решение типового задания
Пример 1. Найти 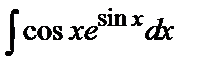 .
.
Решение.Применим метод подстановки. Положим 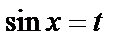 , тогда
, тогда 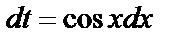 . Используя формулу (6.1), имеем
. Используя формулу (6.1), имеем
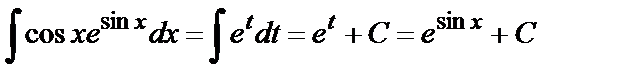 .
.
Пример 2. Найти 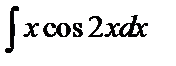 .
.
Решение. Применим метод интегрирования по частям. Положим 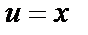 ,
, 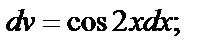 тогда
тогда 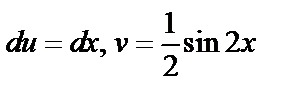 . Используя формулу (6.2), имеем
. Используя формулу (6.2), имеем
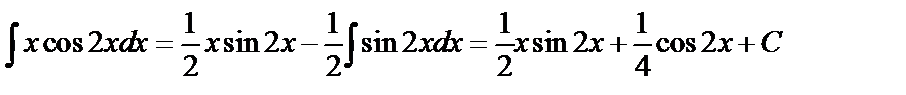 .
.
Пример 3. Найти 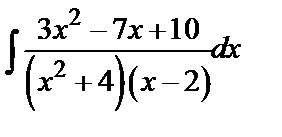 .
.
Решение. Подынтегральная рациональная дробь является правильной и разлагается на элементарные дроби вида (6.3):
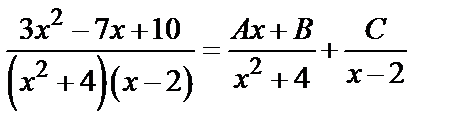 .
.
Освобождаясь от знаменателей в обеих частях этого равенства и приравнивая числители, получаем тождество для вычисления неопределенных коэффициентов 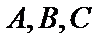 :
:
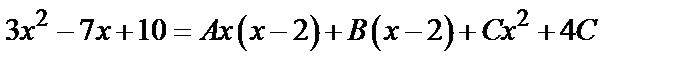 .
.
Составим систему трех уравнений с тремя неизвестными. Одно уравнение получим, полагая х=2 (корень знаменателя подынтегральной функции). Два других получим, приравнивая коэффициенты при одинаковых степенях х в обеих частях тождества, например 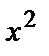 и
и 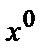 при:
при:
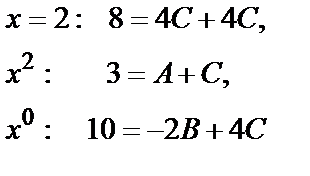
Решение этой системы дает: 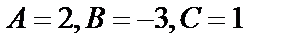 . Таким образом,
. Таким образом,
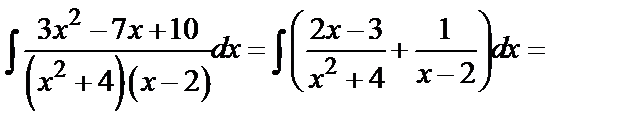

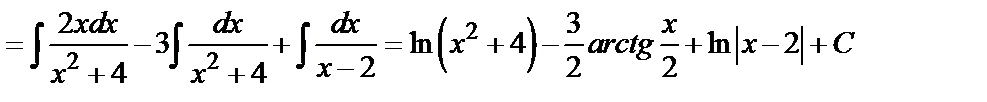 .
.
Дифференциальное исчисление функций нескольких переменных
Функция нескольких переменных. Основные понятия
Пусть даны два непустых множества D и U. Если каждой паре действительных чисел (x; y), принадлежащей множеству D, по определенному правилу ставится в соответствии один и только один элемент u из U, то говорят, что на множестве D задана функция f (или отображение) со множеством значений U. При этом пишут 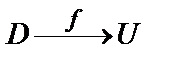 , или
, или 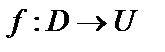 , или
, или 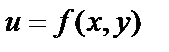 . Множество D называется областью определения функции, а множество U, состоящее из всех чисел вида
. Множество D называется областью определения функции, а множество U, состоящее из всех чисел вида 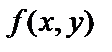 , где
, где 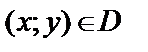 ,
,  множеством значений функции. Значение функции
множеством значений функции. Значение функции 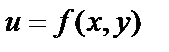 в точке
в точке 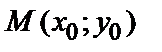 называется частным значением функции и обозначается
называется частным значением функции и обозначается 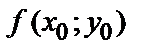 или
или 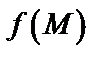 .
.
Дата добавления: 2018-11-26; просмотров: 910;











