Частные производные первого порядка

Частной производной от функции 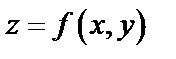по независимой переменной 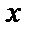называется конечный предел

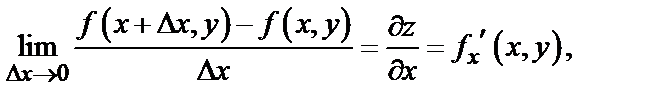
вычисленный при постоянном .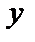

Частной производной по 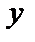называется конечный предел

,

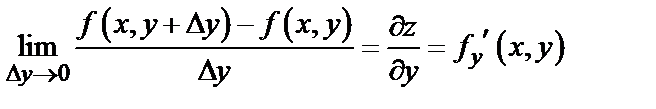вычисленный при постоянном .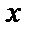

Для частных производных справедливы обычные правила и формулы дифференцирования.

Полный дифференциал

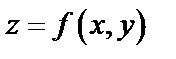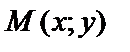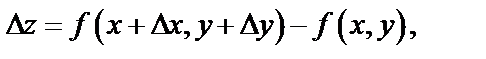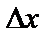Полным приращением функции в точке называется разность где и 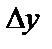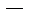произвольные приращения аргументов.

Функция 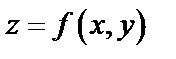называется дифференцируемой в точке 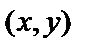, если в этой точке полное приращение можно представить в ви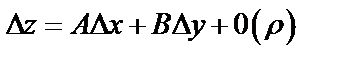де

, где .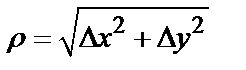

Полным дифференциалом функции 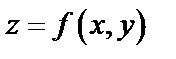называется главная часть полного приращения 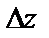, линейная относительно приращений аргументов 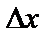и 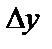, т.е. .

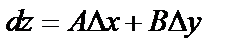Дифференциалы независимых переменных совпадают с их приращениями, т.е. 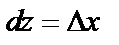и .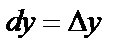

Полный дифференциал функции 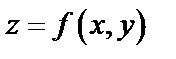вычисляется по формуле

.

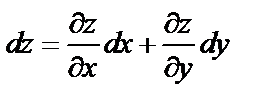Аналогично, полный дифференциал функции трех аргументов 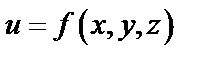вычисляется по формуле

.

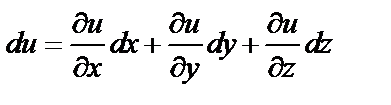При достаточно малом 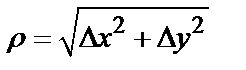для дифференцируемой функции 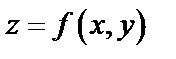справедливы приближенные равенства

.

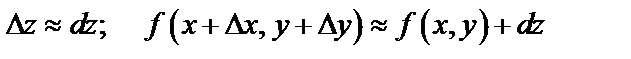или

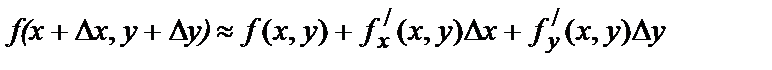. (7.1)