Формулы Ньютона-Котеса.
Численное интегрирование.
Введение.
Требуется найти
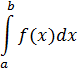
В прикладных задачах этот интеграл может выражать площадь, объём, работу переменной силы и т.д.
Опр. 6.1. Квадратурная формула – приближённое равенство вида
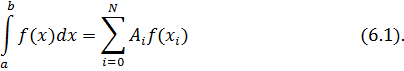
Здесь 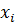 – некоторые точки отрезка
– некоторые точки отрезка 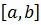 – узлы квадратурной формулы,
– узлы квадратурной формулы, 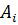 – числовые коэффициенты, называемые весами квадратурной формулы;
– числовые коэффициенты, называемые весами квадратурной формулы; 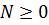 – целое число. Сумма
– целое число. Сумма 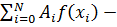 квадратурная сумма, величина
квадратурная сумма, величина 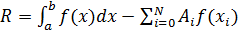 – погрешность квадратурной формулы.
– погрешность квадратурной формулы.
Опр. 6.2.Формула (6.1) точна для многочленов степени m, если для любого многочлена степени не выше m эта формула даёт точное значение интеграла, т.е.
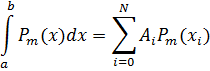
Формулы прямоугольников.
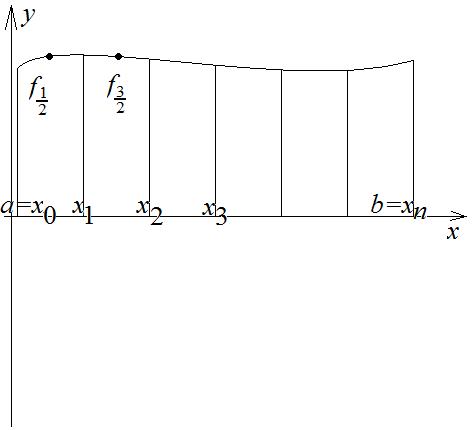
Для простоты шаг 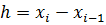 – будем считать постоянным.
– будем считать постоянным.
Элементарная квадратурная формула прямоугольников:
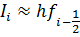
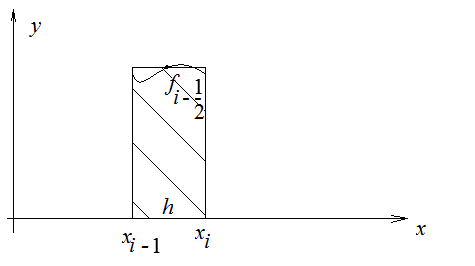
Составная квадратурная формула прямоугольников (центральных прямоугольников):
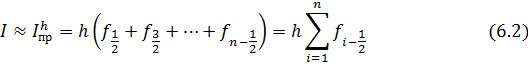
Формула левых прямоугольников:

Формула правых прямоугольников:

Обозначение 6.1.
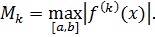
Теорема 6.1. Пусть функция 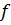 дважды непрерывно дифференцируема на отрезке
дважды непрерывно дифференцируема на отрезке 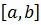 . Тогда
. Тогда
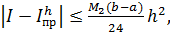 (6.5)
(6.5)
Доказательство.Погрешность формулы прямоугольников
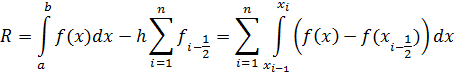
Используя формулу Тейлора
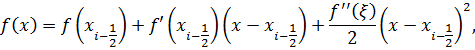
где 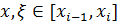 ,
, 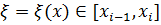 имеем
имеем
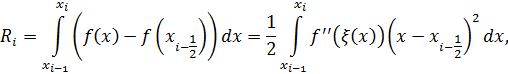
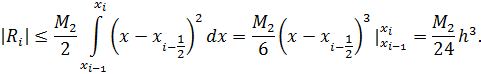
Так как 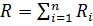 , то
, то 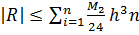 . Замечая, что
. Замечая, что 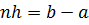 , приходим к оценке (6.5).
, приходим к оценке (6.5).
Формула трапеций.
Элементарная квадратурная формула трапеций:
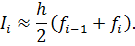
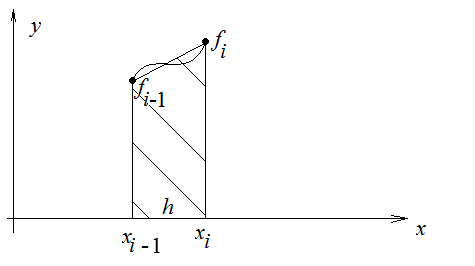
Составная квадратурная формула трапеций:
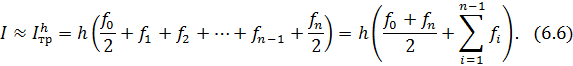
Теорема 6.2. Пусть функция 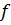 дважды непрерывно дифференцируема на отрезке
дважды непрерывно дифференцируема на отрезке 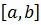 . Тогда
. Тогда
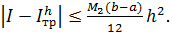 (6.7)
(6.7)
Доказательство: Воспользуемся тем, что отрезок, соединяющий точки 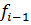 и
и 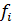 представляет собой график интерполяционного многочлена первой степени
представляет собой график интерполяционного многочлена первой степени 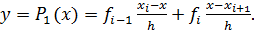 Поэтому
Поэтому
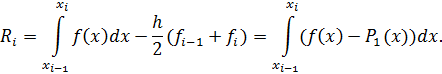
Используя оценку погрешности интерполяции, имеем
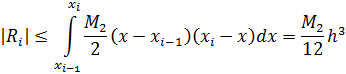
Следовательно,
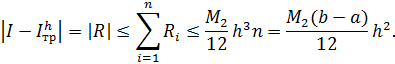
Формула Симпсона.
Элементарная квадратурная формула Симпсона:
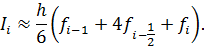
Идея построения. Это так называемая формула парабол. На каждом элементарном отрезке строится интерполяционный многочлен второй степени (парабола), затем этот многочлен интегрируется.
Составная квадратурная формула Симпсона:
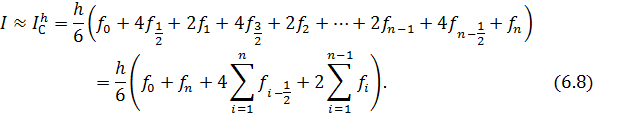
Теорема 6.3. Пусть функция 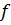 четырежды непрерывно дифференцируема на отрезке
четырежды непрерывно дифференцируема на отрезке 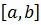 . Тогда
. Тогда
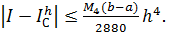 (6.9)
(6.9)
Замечание 6.1.Оценки (6.5), (6.7), (6.9) означают, что формулы прямоугольников и трапеция имеют второй порядок точности относительно 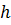 , а формула Симпсона – четвёртый порядок точности. Из тех же оценок следует, что формулы прямоугольников и трапеций точны для многочленов первой степени, а формула Симпсона – для многочленов третьей степени.
, а формула Симпсона – четвёртый порядок точности. Из тех же оценок следует, что формулы прямоугольников и трапеций точны для многочленов первой степени, а формула Симпсона – для многочленов третьей степени.
Формулы (6.3), (6.4) имеют лишь первый порядок точности (абсолютная погрешность каждой из формул не превышает 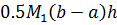 ) и поэтому редко применяются.
) и поэтому редко применяются.
Формулы Ньютона-Котеса.
Идея построения. Интеграл представляют в виде суммы интегралов по элементарным отрезкам. На каждом таком отрезке подынтегральная функция аппроксимируется легко интегрируемой функцией.
В случае, когда аппроксимация осуществляется с помощью интерполяционных многочленов, построенных на основе равноотстоящих значений 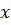 , имеем квадратурные формулы Ньютона-Котеса:
, имеем квадратурные формулы Ньютона-Котеса:
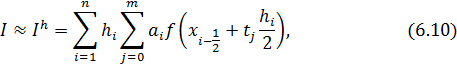
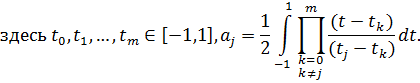
Теорема 6.4. Пусть функция 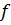 имеет на отрезке
имеет на отрезке 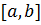 непрерывную производную порядка
непрерывную производную порядка 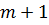 . Тогда для погрешности формулы (6.10) справедлива оценка
. Тогда для погрешности формулы (6.10) справедлива оценка
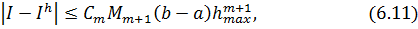
где 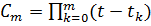 .
.
Дата добавления: 2016-06-05; просмотров: 5278;











