Дискретизация задачи.

Введем сетку по переменному х

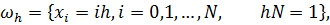
и сетку по переменному t с шагом т, которую обозначим

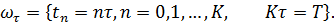
Точки 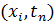, , 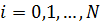, 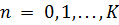образуют узлы пространственно-временной сетки .

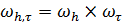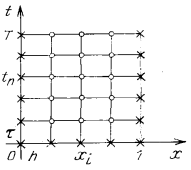
Для функции 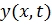, определенной на сетке 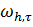, введем обозначения

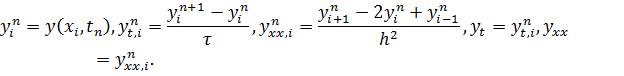
Шаблоны разностных схем: а) явная схема; б — чисто неявная схема; в — симметричная схема:

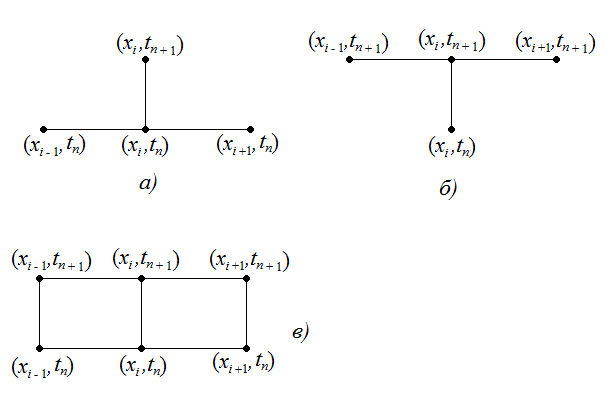
Выбираем шаблон а и заменяем в (10.1) производные разностными выражениями, получим явную разностную схему:

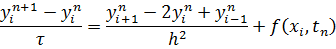
Или

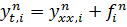
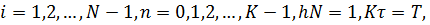
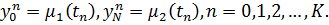
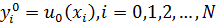
Погрешность аппроксимации явной разностной схемы 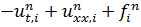: 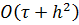(сумма погрешностей вычисления производных).

Утверждение 10.1. Явную разностную схему можно применять лишь при условии устойчивости .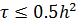

Доказательство.Рассмотрим уравнение

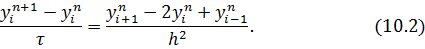
Будем искать частные решения этого уравнения, имеющие вид

где i – мнимая единица, 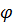- любое действительное число. Подставляя 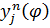в уравнение (10.2) и сокращая на 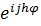, получим

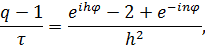
Следовательно,

Если для некоторого 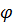множитель 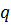станет по модулю больше единицы, то решение такого вида будет неограниченно возрастать при 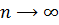. В этом случае разностное уравнение (10.2) называется неустойчивым. Если же 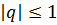для всех действительных 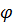, то все решения вида (10.3) ограничены при любом 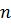и разностное уравнение (10.2) называется устойчивым.

Неравенство 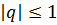выполнено тогда и только тогда, когда 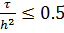или .

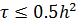Отметим, что для поиска решения явной разностной схемы требуется решить СЛАУ.