Дискретизация задачи. Построение разностной схемы (РС) методом конечных разностей.
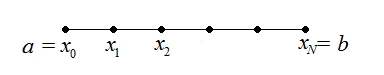
Заменяем отрезок 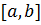 сеткой
сеткой 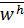 - конечным набором точек
- конечным набором точек  . Точки
. Точки 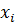 называются узлами сетки. Для простоты изложения будем считать сетку равномерной с шагом
называются узлами сетки. Для простоты изложения будем считать сетку равномерной с шагом 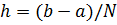 .
.
Сетка 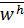 разбивается на два подмножества:
разбивается на два подмножества: 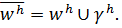 Множество внутренних узлов
Множество внутренних узлов 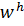 состоит из тех узлов
состоит из тех узлов 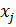 , которые лежат внутри интервала
, которые лежат внутри интервала 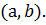 Множество граничных узлов
Множество граничных узлов 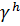 состоит из двух узлов
состоит из двух узлов 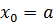 и
и 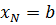 .
.
Мы будем искать решение краевой задачи только в узлах сетки. То есть будем искать не функцию 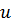 , а сеточную функцию
, а сеточную функцию 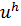 . Значения
. Значения 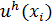 будем обозначать через
будем обозначать через 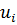 и рассматривать как приближения к значениям
и рассматривать как приближения к значениям 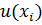 решения задачи (9.1), (9.2).
решения задачи (9.1), (9.2).
Введём также сеточные функции  и
и 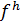 , принимающие в узлах сетки значения
, принимающие в узлах сетки значения 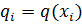 и
и 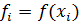 .
.
В (9.1) аппроксимируя 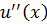 второй разностной производной и заменяя значения функций сеточными аналогами, приходим к задаче
второй разностной производной и заменяя значения функций сеточными аналогами, приходим к задаче
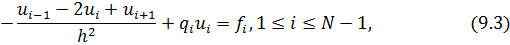

Разрешимость РС. Использование метода прогонки.
Система (9.3), (9.4) приводится к виду
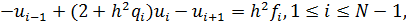
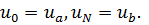
Как нетрудно видеть матрица этой системы трёхдиагональна, то есть её можно решать методом прогонки.
Условия теоремы 3.4. выполняются: 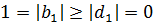 ,
, 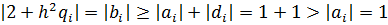 , (1
, (1 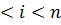 ),
),  . Поэтому прогонка может быть проведена до конца (не один из
. Поэтому прогонка может быть проведена до конца (не один из 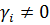 ), и прогонка устойчива, то есть
), и прогонка устойчива, то есть 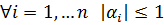 .
.
Исследование РС.
Для сокращения записей далее обозначим
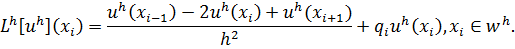
Лемма 9.1. Пусть сеточная функция 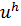 является решением системы сеточных уравнений
является решением системы сеточных уравнений
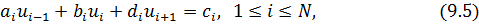
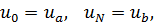
коэффициенты которой удовлетворяют условиям
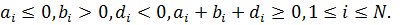
Тогда если 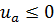 ,
, 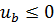 и
и 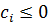 для всех
для всех  то
то 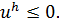
Доказательство. Предположим, что 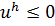 не выполнено. Так как по условию
не выполнено. Так как по условию 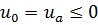 ,
, 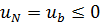 , то максимальное значение функции
, то максимальное значение функции 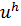 положительно и достигается во внутреннем узле сетки:
положительно и достигается во внутреннем узле сетки: 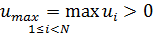 .
.
Пусть j — максимальный среди индексов i, для которых 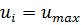 . Тогда
. Тогда 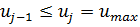 ,
, 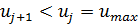
Так как 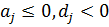 , то
, то 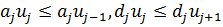 . Учитывая, что
. Учитывая, что 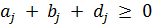 ,
, 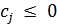 , из равенства (9.5), взятого при
, из равенства (9.5), взятого при 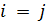 , получим
, получим
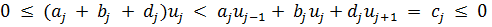
Полученное противоречие (0 < 0) доказывает, что 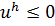 .
.
Теорема 9.1. (принцип максимума). Пусть сеточная функция 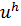 является решением разностной схемы
является решением разностной схемы
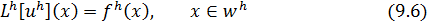
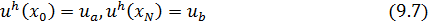
Тогда если 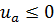 ,
, 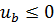 и
и 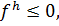 то
то 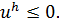
Доказательство.Легко проверяется, что коэффициенты системы сеточных уравнений (9.6), (9.7) удовлетворяют условиям леммы 9.1.
Теорема 9.2. Для решения разностной схемы 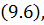
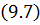 справедлива априорная оценка
справедлива априорная оценка
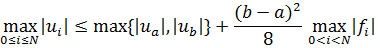
Дата добавления: 2016-06-05; просмотров: 3016;











