Явный метод Эйлера.

Отбрасывая остаточный член формулы Тейлора, получим приближённое равенство

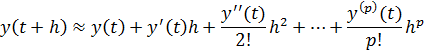
При 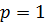, имеем

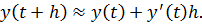
В силу равенства (8.1), имеем

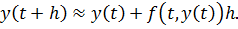
Или

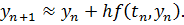
Метод Эйлера:

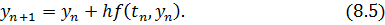
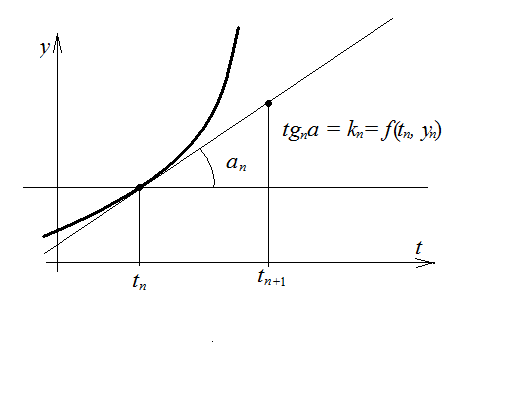
Геометрическая интерпретация одного шага метода Эйлера состоит в аппроксимации решения на 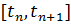касательной .

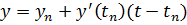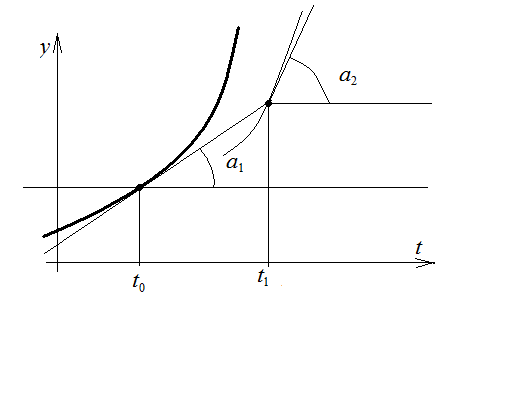
Таким образом, после N шагов получаем ломанную Эйлера:

Чтобы определить погрешность аппроксимации метода Эйлера запишем формулу Тейлора с остаточным членом:

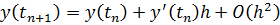
или, в силу равенства (8.1):

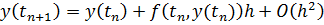
Поэтому погрешностью аппроксимации для метода Эйлера:

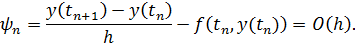
То есть метод Эйлера имеет первый порядок аппроксимации.

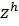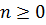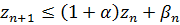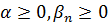Лемма 8.1. Пусть - неотрицательная сеточная функция, удовлетворяющая для всех неравенству , где . Тогда при всех 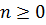верна оценка

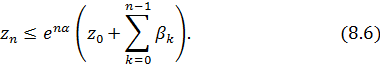
Доказательство. По индукции. При 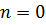неравенство (11.6) превращается в очевидное .

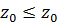Пусть (8.6) выполнено при некотором 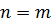. Тогда, использую оценк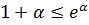и и 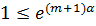, получим следующую цепочку неравенств:

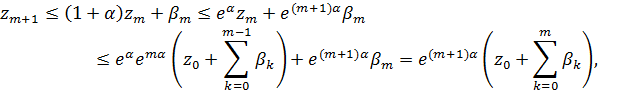
то есть (8.6) верно и при 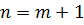. Итак, (8.6) верно при всех n. Ч.т.д.

Пусть 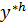- решение возмущённой дискретной задачи Коши:

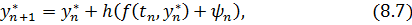
Теорема 8.2. Пусть f удовлетворяет условию 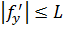. Тогда справедливо:

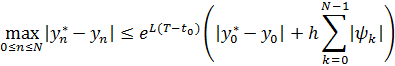
означающее, что метод Эйлера устойчив на конечном отрезке.

Доказательство. Вычитая из уравнения (8.7) уравнение (8.5) и пользуясь формулой конечных приращений Лагранжа

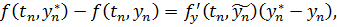
получаем равенство

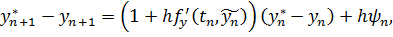
откуда следует

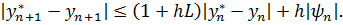
Обозначим 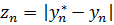, , 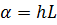, 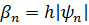тогда 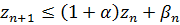. Согласно, лемме 8.1, имеем

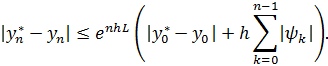
Учитывая, что 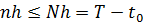, приходим к равенству из условия теоремы 8.2.