Без доказательства.
Коснёмся устойчивости РС.
Пусть 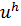 - решение разностной схемы
- решение разностной схемы 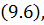
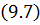 , а и
, а и 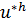 — решение разностной схемы
— решение разностной схемы
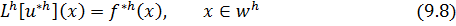
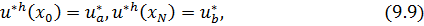
где 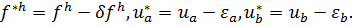
Разностная схема 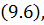
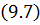 устойчива, если при любых
устойчива, если при любых 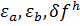 справедлива оценка
справедлива оценка
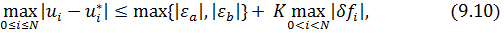
где постоянная К не зависит от h.
Теорема 9.3. (об устойчивости разностной схемы). Для разностной схемы 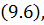
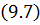 справедлива оценка (9.10) с постоянной
справедлива оценка (9.10) с постоянной 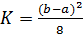 .
.
Доказательство. Заметим, что сеточная функция 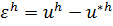 является решением разностной схемы
является решением разностной схемы
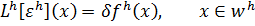
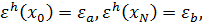
Применяя для оценивания 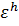 приходим к нужному неравенству.
приходим к нужному неравенству.
Определение 9.1. Пусть 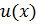 - решение дифференциального уравнения
- решение дифференциального уравнения

Сеточная функция 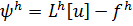 называется погрешностью аппроксимации разностного уравнения
называется погрешностью аппроксимации разностного уравнения

Определение 9.2. Говорят, что разностное уравнение (9.12) аппроксимирует дифференциальное уравнение (9.11), если 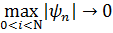 при
при 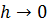 , и аппроксимирует его с m-м порядком, если справедлива оценка
, и аппроксимирует его с m-м порядком, если справедлива оценка 
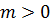 .
.
Теорема 9.4. Пусть коэффициенты q и f дважды непрерывно дифференцируемы на отрезке 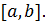 Тогда разностное уравнение
Тогда разностное уравнение 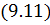 аппроксимирует дифференциальное уравнение
аппроксимирует дифференциальное уравнение 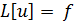 со вторым порядком, причем справедлива оценка
со вторым порядком, причем справедлива оценка
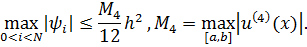
Доказательство. Прежде всего заметим, что в силу наших знаний по дифференциальным уравнениям функция 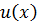 имеет на отрезке
имеет на отрезке 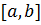 непрерывную производную
непрерывную производную 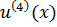 .
.
В силу определения погрешности аппроксимации имеем
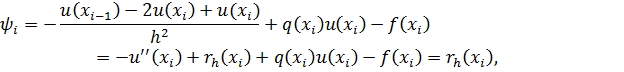
где 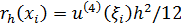 - погрешность аппроксимации производной
- погрешность аппроксимации производной 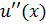 разностной формулой (2-я разностная производная). Таким образом,
разностной формулой (2-я разностная производная). Таким образом,
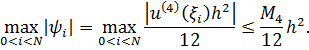
Определение 9.3. Пусть 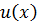 — решение краевой задачи, а
— решение краевой задачи, а 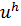 — решение соответствующей разностной схемы. Назовем погрешностью разностной схемы сеточную функцию
— решение соответствующей разностной схемы. Назовем погрешностью разностной схемы сеточную функцию 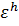 , принимающую значения
, принимающую значения  в узлах сетки.
в узлах сетки.
Определение 9.4. Разностная схема сходится при 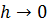 , если
, если 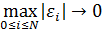 при
при 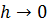 , и сходится с m-м порядком точности (при
, и сходится с m-м порядком точности (при 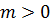 ), если
), если 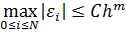 , где C некоторая постоянная, не зависящая от h.
, где C некоторая постоянная, не зависящая от h.
Теорема 9.5. Пусть функции q и f дважды непрерывно дифференцируемы на отрезке 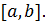 Тогда справедлива оценка
Тогда справедлива оценка
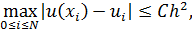
где 
Доказательство.Введем сеточную функцию 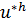 , значения которой в узлах сетки совпадают с точными значениями решения краевой задачи, т. е.
, значения которой в узлах сетки совпадают с точными значениями решения краевой задачи, т. е.
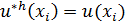 . Функцию
. Функцию 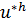 можно рассматривать как решение разностной схемы (9.8),(9.9), где
можно рассматривать как решение разностной схемы (9.8),(9.9), где 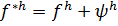 ,
, 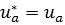 ,
, 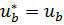 . В силу теоремы 9.3 для
. В силу теоремы 9.3 для 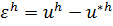 справедлива оценка
справедлива оценка
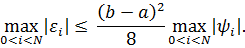
Далее с помощью теоремы 9.4 получаем оценку из условия теоремы 9.5.
Замечание 9.1. Мы показали, что разностная схема (9.6), (9.7) сходится со вторым порядком точности.
Замечание 9.2. Пусть 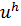 и
и 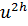 — решения разностной схемы (9.6), (9.7), соответствующие шагам
— решения разностной схемы (9.6), (9.7), соответствующие шагам 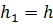 и
и 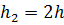 . Тогда в соответствии с правилом Рунге при определенных условиях справедлива приближенная формула
. Тогда в соответствии с правилом Рунге при определенных условиях справедлива приближенная формула
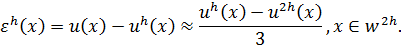
Отметим, что она применима только в узлах сетки 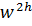 , т. е. там, где определены обе сеточные функции
, т. е. там, где определены обе сеточные функции 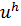 и
и 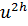 .
.
Дата добавления: 2016-06-05; просмотров: 2611;











