Дискретизация задачи.

Заменяем отрезок 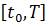конечным множеством точек 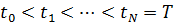, называемым сеткой 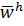. Как правило, будем рассматривать сетки, для которых 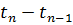постоянен. В этом случае 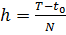и

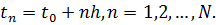
Далее мы будем рассматривать функции, которые определены только в узлах сетки. Для того чтобы отличать такие функции от функций непрерывного аргумента будем помечать их с помощью индекса h. Например, 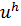- сеточная функция. Для краткости будем обозначать .

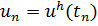Далее заменяем 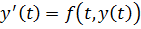уравнением вида

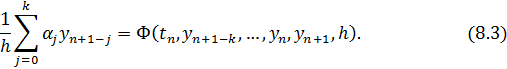
В (8.3) входят значения сеточной функции 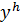в 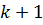последовательных точках 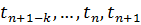. Предполагается, что 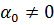. Левую часть (8.3) можно рассматривать как аппроксимацию 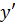, а правую часть – как аппроксимацию .

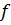Значение 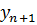приближённого решения в очередной точке находится из (8.3). При этом используются k значений 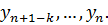Такие методы называются k-шаговыми.

Проблема страта: необходимо задать k начальных значений

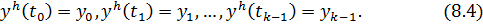
Задачу вычисления сеточной функции 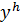, удовлетворяющей при всех 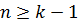уравнению (8.3) и принимающей заданные начальные значения (8.4), будем называть дискретной задачей Коши. Уравнение (8.3) задаёт численный метод решения задачи Коши.

При 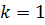уравнение (8.3) упрощается и принимает вид

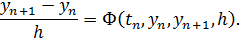
Соответствующий метод принято называть одношаговым. Вычисление 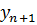осуществляется с использованием только одного предыдущего значения 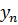. Поэтому одношаговые методы называют самостартующими.

Определение 8.2. Если функция 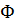из уравнения (8.3) не зависит от 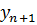, соответствующий метод называется явным. Методы, в которых функция 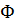зависит от 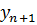, называются неявными.

Замечание 8.3.При реализации неявных методов приходится решать относительно 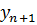нелинейное уравнение (8.3).

Пример 8.1. Примером явного метода является метод Эйлера:

.

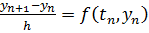Примером неявного метода является неявный метод Эйлера:

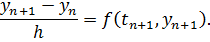
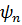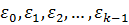Определение 8.3. Внесём в правую часть (8.3) и в (8.4) произвольные малые возмущения и соответственно. Положим 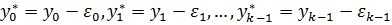. Пусть 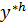- решение возмущённой задачи

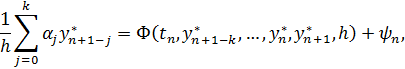
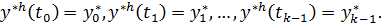
Дискретная задача Коши (8.3), (8.4) и соответствующий численный метод называются устойчивыми, если при всех 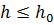(где 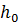достаточно мало) справедливо неравенство

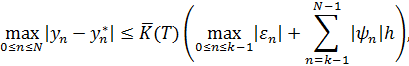
где величина 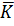не зависит от 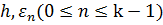и .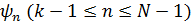

Уточнение 8.1.Пусть 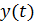– произвольная гладкая функция. Зафиксируем 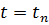, устремим h к нулю, n – к бесконечности. Предположим, что коэффициенты из (8.3) удовлетворяют условиям:

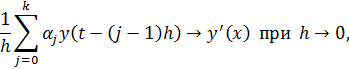
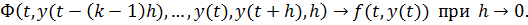
Определение 8.4. Пусть y(t) – решение задачи Коши (8.1), (8.2). Погрешностью аппроксимации дискретного уравнения (8.3) на решении y называется сеточная функция 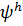, определяемая формулой:

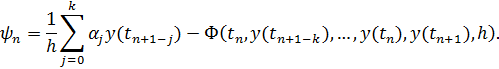
Определение 8.5. Говорят, что дискретное уравнение (8.3) аппроксимирует дифференциальное уравнение (8.1), есл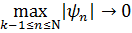и при 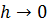, и аппроксимирует его с p-м порядком, если справедлива оценка .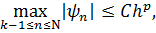

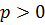Определение 8.6. Пусть 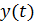– решение задачи Коши. Глобальной погрешностью (или просто погрешностью) численного метода называется сеточная функция 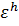со значениями 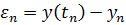в узлах 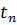. В качестве меры абсолютной погрешности метода примем величину .

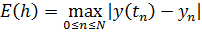Численный метод решения задачи Коши называется сходящимся, если для него 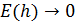при 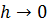. Метод сходится с p-м порядком точности, если справедлива оценка , .

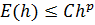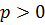Теорема 8.1. Пусть численный метод устойчив на конечном отрезке и имеет порядок аппроксимации равный p. Тогда если начальные значения 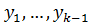заданы с p-м порядком точности, то и метод сходится с p-м порядком точности.