Левая, правая и центральные разностные производные.

Требуется найти .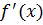

Численное дифференцирование применяется тогда, когда функцию невозможно продифференцировать аналитически. Это происходит, например, когда функция задана таблицей. Кроме того, формулы численного дифференцирования используются при разработке вычислительных методов решения многих задач.

Предположим, что в окрестности точки x функция f дифференцируема достаточное число раз. По определению,

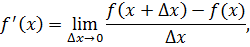
естественно попытаться использовать для вычисления 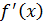формулы:

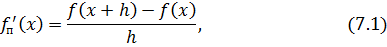
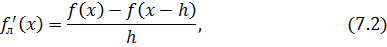
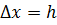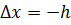соответствующие выбору фиксированных значений и . Здесь 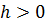– малый параметр (шаг). Правые части формул (7.1) и (7.2) часто называют правой и левой разностными производными.

Центральная разностная производная:

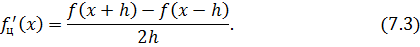
Для оценки погрешностей воспользуемся формулой Тейлора:

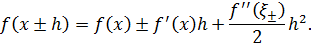
Здесь и ниже 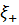и 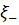- некоторые точки, расположенные на 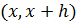и 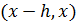соответственно. Имеем,

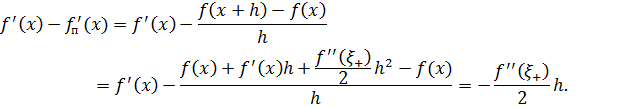
Итак,

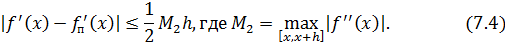
Аналогично устанавливается, что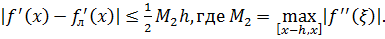

Для оценки погрешностей формулы 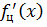также воспользуемся формулой Тейлора:

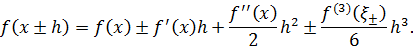
Получим,

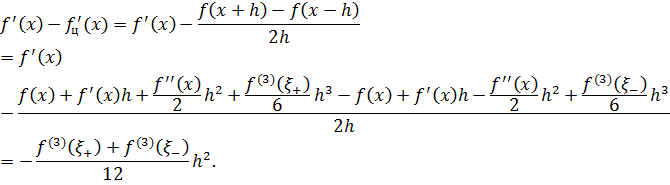
Итак,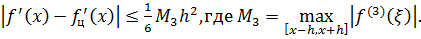

Таким образом, формулы (7.1) и (7.2) имеют первый порядок точности по 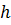. Иначе говоря, правая и левая разностные производные аппроксимируют 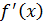с первым порядком точности относительно 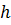, а центральная разностная производная – со вторым порядком.