Рациональные корни многочлена с целыми коэффициентами
Вопрос о нахождении рациональных корней многочлена f(x)  Q[x] (с рациональными коэффициентами) сводится к вопросу об отыскании рациональных корней многочленов k ∙ f(x)
Q[x] (с рациональными коэффициентами) сводится к вопросу об отыскании рациональных корней многочленов k ∙ f(x)  Z[x] (с целыми коэффициентами). Здесь число k является наименьшим общим кратным знаменателей коэффициентов данного многочлена.
Z[x] (с целыми коэффициентами). Здесь число k является наименьшим общим кратным знаменателей коэффициентов данного многочлена.
Необходимые, но не достаточные условия существования рациональных корней многочлена с целыми коэффициентами дает следующая теорема.
Теорема 6.1 (о рациональных корнях многочлена с целыми коэффициентами). Если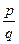 –рациональный корень многочлена f(x)=an × xn+ + …+ a1 × x + a0сцелымикоэффициентами, причем (p, q) = 1, то числитель дроби p является делителем свободного члена а0, а знаменатель q является делителем старшего коэффициента а0.
–рациональный корень многочлена f(x)=an × xn+ + …+ a1 × x + a0сцелымикоэффициентами, причем (p, q) = 1, то числитель дроби p является делителем свободного члена а0, а знаменатель q является делителем старшего коэффициента а0.
Теорема 6.2.Если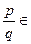 Q (где(p, q) =1) является рациональным корнем многочлена f(x) с целыми коэффициентами, то
Q (где(p, q) =1) является рациональным корнем многочлена f(x) с целыми коэффициентами, то 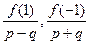 – целые числа.
– целые числа.
Пример.Найтивсе рациональные корнимногочлена
f(x) = 6 x4 + x3 + 2 x2 – 4 х+ 1.
1. По теореме 6.1: если 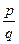 –рациональный корень многочлена f(x), (где(p, q) = 1),то a0 = 1
–рациональный корень многочлена f(x), (где(p, q) = 1),то a0 = 1 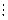 p, an = 6
p, an = 6 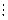 q. Поэтому p
q. Поэтому p  {
{ 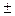 1}, q
1}, q  {1, 2, 3, 6}, значит,
{1, 2, 3, 6}, значит,
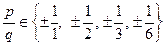 .
.
2. Известно, что (следствие 5.3) число а является корнем многочлена f(x) тогда и только тогда, когда f(x) делится на (х – а).
Следовательно, для проверки того, являются ли числа 1 и –1 корнями многочлена f(x) можно воспользоваться схемой Горнера:
| – 4 | |||||
| – 1 | – 5 | –11 |
f(1) = 6 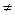 0, f(–1) = 12
0, f(–1) = 12 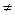 0, поэтому 1 и –1 не являются корнями многочлена f(x).
0, поэтому 1 и –1 не являются корнями многочлена f(x).
3. Чтобы отсеять часть оставшихся чисел 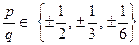 , воспользуемся теоремой 6.2. Если выражения
, воспользуемся теоремой 6.2. Если выражения 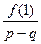 или
или 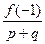 принимает целые значения для соответствующих значений числителя p и знаменателя q, то в соответствующих клетках таблицы (см. ниже) будем писать букву “ц”, в противном случае – “др”.
принимает целые значения для соответствующих значений числителя p и знаменателя q, то в соответствующих клетках таблицы (см. ниже) будем писать букву “ц”, в противном случае – “др”.
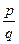
| 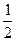
| 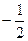
| 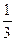
| 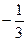
| 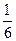
| 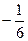
|
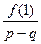 = = 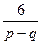
| ц | ц | ц | др | др | др |
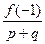 = = 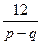
| ц | ц | ц | ц | др | др |
4. С помощью схемы Горнера проверяем, будут ли оставшиеся после отсеивания числа 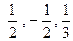 корнями f(x). Вначале разделим f(x) на (х –
корнями f(x). Вначале разделим f(x) на (х – 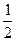 ).
).
| – 4 | |||||
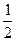
| –2 |
В результате имеем: f(x) = (х – 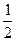 )(6 x3 + 4 x2 + 4 х – 2) и
)(6 x3 + 4 x2 + 4 х – 2) и 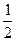 – корень f(x). Частное q(x) = 6 x3 + 4 x2 + 4 х – 2 разделим на (х +
– корень f(x). Частное q(x) = 6 x3 + 4 x2 + 4 х – 2 разделим на (х + 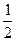 ).
).
| – 4 | |||||
– 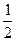
| –2 | –5 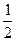
| 3 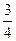
|
Так как q (– 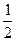 ) = 3
) = 3 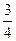
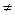 0, то (–
0, то (– 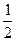 ) не является корнем многочлена q(x), а значит и многочлена f(x).
) не является корнем многочлена q(x), а значит и многочлена f(x).
Наконец, разделим многочлен q(x) = 6 x3 + 4 x2 + + 4 х – 2 на (х – 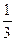 ).
).
| – 4 | |||||
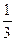
| –3 |
Получили: q ( 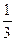 ) = 0, т.е.
) = 0, т.е. 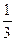 – корень q(x), а значит,
– корень q(x), а значит, 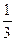 – корень f (x). Таким образом, многочлен f (x) имеет два рациональных корня:
– корень f (x). Таким образом, многочлен f (x) имеет два рациональных корня: 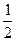 и
и 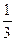 .
.
Дата добавления: 2021-12-14; просмотров: 692;











