Деление многочлена на двучлен. Теорема Безу.
Схема Горнера
Пусть f(x)=anxn+an-1xn-1+…+a1x+a0ÎР[х], aÎР – произвольный элемент поля Р. Тогда f(a)=anan+an-1an-1+…+a1a+a0 называется значением многочлена f(x) при х=a. В частности, если f(a)=0, то a называется корнем многочлена f(x). Интересные результаты получаются при делении многочлена на двучлен, то есть на многочлен вида (х-с).
Теорема Безу. Остаток от деления многочлена f(x) на двучлен (х-с) равен значению этого многочлена при х=с.
Доказательство
По теореме о делении с остатком можно представить
f(x)= (х-с) q(x)+ r(x) и r(x)=0 или deg r(x)< deg(х-с)=1, то есть deg r(x)=0, следовательно, r(x)= r - многочлен нулевой степени. При х=с получим
f(с)= (с-с) q(с)+ rÛ f(с)= r. Теорема доказана.
Следствие. х=a будет корнем многочлена f(x) тогда и только тогда, когда многочлен f(x) делится на двучлен х-a нацело.
Доказательство
По теореме Безу f(a)=r. Если r=0, то f(a)=0, то есть a - корень. Обратно, если a - корень, то f(a)=0, следовательно, r=f(a)=0.
Теорема 4. Многочлен n-ой степени имеет не более n различных корней.
Доказательство. Докажем методом математической индукции по степени многочлена.
Пусть n=1, тогда f(x)=ax+b. Очевидно, найти корни многочлена – это решить уравнение ax+b=0, а так как многочлен задан над полем, то такое уравнение однозначно разрешимо при любом а¹0, то есть при n=1 теорема верна.
Предположим, что теорема верна при любом k<n, и рассмотрим многочлен n-ой степени f(x). Если f(x) не имеет корней, то теорема верна. Если f(x) имеет хотя бы один корень с0, тогда по следствию из теоремы Безу, f(x)=(х-с0) q(x), где q(x) - многочлен степени n-1<n. Очевидно, что любой корень многочлена f(x), отличный от с0, является также корнем многочлена q(x) и, наоборот, любой корень многочлена q(x) является также корнем многочлена f(x), а согласно индуктивному предположению, многочлен q(x) имеет не более n-1 корня, тогда многочлен f(x) имеет не более (n-1)+1= n корней, то есть теорема верна, следовательно, она верна для любого натурального числа n.
Следствие. Пусть f(x), g(x)ÎР[х] и deg f(x)=deg g(x)= n. Если значения этих многочленов равны более, чем при n различных значениях переменной х, то f(x)=g(x).
Доказательство. Пусть
f(с1)=g(с1)
f(с2)=g(с2)
………….
f(сn)=g(сn)
f(сn+1)=g(сn+1).
Рассмотрим многочлен h(x)=f(x)-g(x). Очевидно, что степень этого многочлена меньше или равна n и h(x) имеет больше, чем n корней, следовательно, по доказанной теореме, h(x)=0Û f(x)-g(x)=0Û f(x) =g(x).
Выведем правило для вычисления коэффициентов частного при делении f(x) на (х-с). Обозначим частное q(x)= bn-1xn-1+bn-2xn-2+…+b1x+b0 и преобразуем равенство f(x)= (х-с) q(x)+ r, считая, что f(x)=anxn+an-1xn-1+…+a1x+a0, q(x)= bn-1xn-1+bn-2xn-2+…+b1x+b0, r= f(с).
f(x)=(х-с)q(x)+rÛ anxn+an-1xn-1+…+a1x+a0=(х-с)(bn-1xn-1+bn-2xn-2+…+b1x+b0)+f(с).
Û anxn+an-1xn-1+…+a1x+a0= bn-1xn+(bn-2-сbn-1)xn-1+…+(b0-сb1)x+(f(с)-сb0).
По определению равенства многочленов получаем
an= bn-1,
an-1=bn-2-сbn-1,
…………….,
a1=b0-сb1,
a0=f(с)-сb0.
Откуда
bn-1= an,
bn-2= an-1+сbn-1,
……………., (8)
b0= a1 +сb1,
f(с) = a0+сb0.
Получили алгоритм вычисления коэффициентов частного при делении f(x) на (х-с), известный как схема Горнера.
Вычисления по схеме Горнера удобно записывать в виде таблицы, в верхней строке которой записывают коэффициенты делимого, а в нижней получают коэффициенты частного, вычисляемые по формулам (8).
| an | an-1 | ……………… | a1 | a0 | |
| х=с | bn-1= an | bn-2= an-1+сbn-1 | ……………… | b0= a1 +сb1 | f(с) = a0+сb0. |
Пример. Разделить f(x)=2x5+x4-3x2+4x-5 на g(x)=x-2. Делим по схеме Горнера.
Обратите внимание! коэффициент при х3 равен 0. При вычислении по алгоритму его нужно учитывать!
 2 2
| -3 | -5 | ||||
| х=2 | 2*2+1=5 | 2*5+0=10 | 2*10-3=17 | 2*17+4=38 | 2*38-5=71 |
Получили f(x)=(x-2)(2x4+5x3 +10x2+17x+38)+71, кроме того, на основании теоремы Безу, можно сразу сказать, что f(2)=71.
Схему Горнера удобно использовать для решения различных задач. Так, мы уже показали, как можно найти частное и остаток от деления f(x) на х-с, как можно найти значение f(с). Приведем еще несколько примеров.
Схема Горнера удобна при разложении данного многочлена 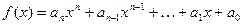 по степеням двучлена
по степеням двучлена 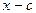 . Пусть
. Пусть
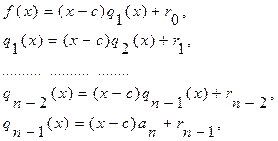 (9)
(9)
где 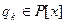 и
и 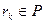 . Если последнее выражение в (9) для
. Если последнее выражение в (9) для 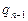 подставить в предыдущее равенство, а затем то, что при этом получится, подставить вместо
подставить в предыдущее равенство, а затем то, что при этом получится, подставить вместо 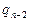 и т.д., то придем к равенству
и т.д., то придем к равенству
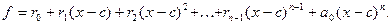 (10)
(10)
Это есть разложение данного многочлена f (х) по степеням (x - c). Пусть Р - поле. Дифференцируя обе части равенства (10) и полагая 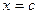 , получим
, получим 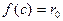 ,
, 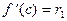 ,
, 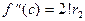 , ...,
, ..., 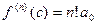 . Поэтому равенство (10) можно записать в виде
. Поэтому равенство (10) можно записать в виде
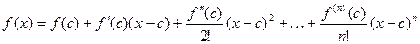 ,
,
если только f - многочлен над полем нулевой характеристики. Это и есть формула Тейлора для многочленов, известная из курса математического анализа.
Все вычисления удобно расположить в одну таблицу.
| a0 | a1 | ... | an-2 | an-1 | an | |
| c | b0 | b1 | ... | bn-1 | 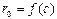
| |
| c0 | c1 | ... | 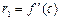
| |||
| d0 | d1 | ... | 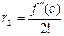
| |||
| ... | ... | ... | ... | ... | ... | |
| a0 | 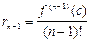
|
Пример. Разложить многочлен f(x)= 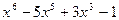 по степеням
по степеням 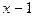 . Найти значения функции f(x) и всех ее производных при х=1. Для этого построим таблицу.
. Найти значения функции f(x) и всех ее производных при х=1. Для этого построим таблицу.
| -5 | -1 | ||||||
| х=1 | -4 | -4 | -1 | -1 | -1 | -2 | |
| х=1 | -3 | -7 | -8 | -9 | -10 | ||
| х=1 | -2 | -9 | -17 | -26 | |||
| х=1 | -1 | -10 | -27 | ||||
| х=1 | -10 | ||||||
| х=1 | |||||||
| х=1 |
Получили 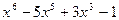 =(x-1)6+(x-1)5-10(x-1)4-27(x-1)3-26(x-1)2-10(x-1)-2.
=(x-1)6+(x-1)5-10(x-1)4-27(x-1)3-26(x-1)2-10(x-1)-2.
Значения производных найдем из условия:
f(1)=-2; f’(1)=(-10)*1!=-10; f’’(x)=(-26)*2!=-52; f’’’(1)=(-27)*3!=-162; fiv(1)=(-10)*4!=-240; fv(1)=1*5!=120; fvi(1)=1*6!=720.
Упражнение Разложить по степеням 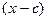 :
:
1) 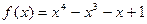 ,
, 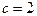 ;
;
2) 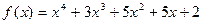 ,
, 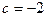 ;
;
3) 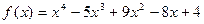 ,
, 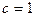 ;
;
4) 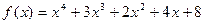 ,
, 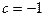 ;
;
5) 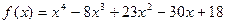 ,
, 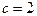 ;
;
6) 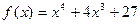 ,
, 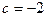 ;
;
7) 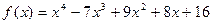 ,
, 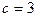 ;
;
8) 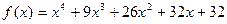 ,
, 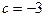 ;
;
9) 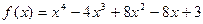 ,
, 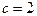 ;
;
10) 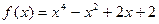 ,
, 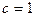 ;
;
11) 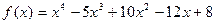 ,
, 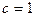 ;
;
12) 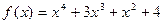 ,
, 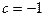 ;
;
13) 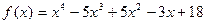 ,
, 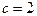 ;
;
14) 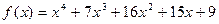 ,
, 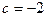 .
.
Дата добавления: 2020-10-25; просмотров: 1179;











