VI. Закрепление изученного материала

VII. Самостоятельная работа

VIII. Подведение итогов урока

IX. Постановка домашнего задания

Билет № 18. Наибольший общий делитель и наименьшее общее кратное

Целых чисел

Понятие НОД целых чисел

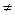Определение 8.1.Целое число d Z, (d 0)называется общим делителем чисел a₁, a₂, … , a_k , если каждое а_i (i = 1, 2, …. , k) делится на d.

Определение 8.2.Целое число d Z (d 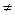0) называется наибольшим общим делителем чисел a₁, a₂, … , a_k, если

1. d – общий делитель всех а_i;

2. d делится на любой другой общий делитель этих чисел.

Обозначение: НОД (а₁, а₂, … , а_n) = d.

Теорема 8.1. Наибольший общий делитель целых чисел а и b определяется однозначно с точностью до знака.

Доказательство.

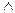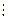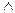Пусть d₁ = (a, b) d₂ = (a, b) d₁ d₂ d₂ 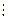d₁ [(d₁ = d₂) 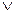(d₁ = – d₂)].

Замечание.Обычно берется положительное значение d = (a, b).

Пример.Даны числа: 9, 18, 27, 54. Числа 3 и 9 являются общими делителями этих чисел, т.е. НОД (9, 18, 27, 54) = 9.

Рассмотрим метод, который позволяет доказать существование НОД (а, b) и находить его для любой пары целых чисел, его называют алгоритмом Евклида. Он основан на трех леммах.

Лемма 8.2. Еслиа 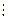b, то (а, b) = b.

Лемма 8.3.Если а = bq + r, где а, b, r отличны от 0, то (а, b) = (b, r).

Алгоритм Евклида

1-й шаг. Делим а на b 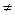0. Если а 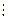b, то (а, b) = b по лемме 8.2. Если а = bq₀ + r₁, то (а, b) = (b, r₁).

2-й шаг. Делим b на r₁. Если b 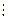r₁ , то (b, r₁) = r₁. Если b = r₁q₁ + r₂, то (b, r₁) = (r₁, r₂).

3-й шаг. Делим r₁ на r₂ b и т.д.

Лемма 8.4.Алгоритм Евклида состоит из конечного числа шагов.

Действительно, остатки, получаемые в процессе деления убывают и являются натуральными числами | b | < r₁ < r₂ < …, поэтому не более, чем за | b | шагов получим остаток равный нулю, т.е. (r_n-1, r_n) = r_n и тогда (r_n-1, r_n) = r_n.

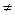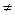Теорема 8.5 (о нахождении НОД(а, b) с помощью алгоритма Евклида).Последнийотличный от нуля остаток валгоритме Евклида является наибольшим общим делителем целых чисел а и b (а 0, b 0).

Доказательство. Применим к числам a и b алгоритм Евклида:

а = bq₀ + r₁, 0 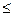r₁ < b

b = r₁q + r₂, 0 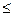r₂ < r₁

………………………….

r_n-2 = r_n-1 ∙ q_n-1 + r_n, 0 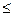r_n < r_n-1

r_n-1 = r_n ∙ q_n + 0

Из первого равенства по лемме 8.3 будем иметь (а, b) = (b, r₁). Из второго равенства алгоритма Евклида по лемме 8.3 будем иметь: (b, r₁) = (r₁, r₂) и т.д.

Из последнего равенства (r_n-1, r_n) = r_n.

Итак, (а, b) = r_n.

Пример.ВычислимНОД (154, 48) с помощью алгоритма Евклида.

_ 154 | 48

144 3

_ 48 | 10

40 4

_10 | 8

8 1

_ 8 | 2

8 4

Процесс деления можно записывать в виде последовательности равенств деления с остатком, называемой последовательностью Евклида.

154 = 48 ∙ 3 + 10

48 = 10 ∙ 4 +8

10 = 8 ∙ 1 + 2

8 = 2 ∙ 4

Итак, НОД (154, 48) = 2.

Следствие 1 (о линейном разложении НОД(a, b)).Наибольший общий делитель НОД(a, b) любых целых чисел a 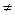0, b 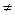0 можно представить в виде линейной комбинации чисел a и b c целыми коэффициентами u и v: НОД(a, b) = u ∙ a + v ∙ b (1)

Определение 8.3.Представление(1)называется линейным разложением наибольшего общего делителя чисел a и b.

Пример. Найдем линейное представление НОД(154, 48). Воспользуемся последовательностью Евклида из предыдущего примера, выразим остатки: 2 = 10 + 8 ∙ (-1), 8 = 48 + 10 ∙ (-4), 10 = 154 + 48 ∙ (-3). Подставим в первое равенство выражение 8 из второго, затем для 10 из третьего, получаем: 2 = 10 + [48 + 10∙ (-4)] ∙ (-1) = 48 ∙ (-1) + 10 ∙ 5 = 48 ∙ (-1) + [154 + 48 ∙ (-3)] ∙ 5 = 154 ∙ 5 + 48 ∙ (-16).

Итак, 154 ∙ 5 + 48 ∙ (-16) = 2 – линейное разложение (154, 48).