Выбор образующего многочлена

Многочлены бывают приводимыми и неприводимыми. Многочлен, который можно представить в виде произведения многочленов низших степеней, называют приводимым, в противном случае – неприводимым. В табл. 2.3 в качестве примера указаны все неприводимые многочлены до шестой степени включительно (на практике используются многочлены и более высоких степеней).

Таблица 2.3

Неприводимые многочлены и их двоичные эквиваленты

Многочлен	Эквивалент	Многочлен	Эквивалент

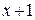
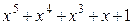
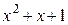
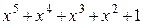
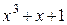
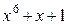
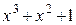
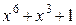
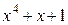
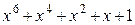
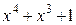
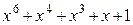
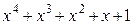
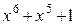
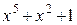
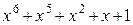
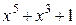
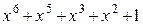
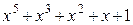
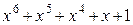
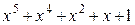
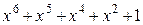
В основу циклического кодирования положено использование неприводимых многочленов, которые применительно к циклическим кодам называют образующими.

Обозначим образующий многочлен через .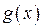

Все КВ образующей матрицы (2.26) являются разрешенными и, следовательно, 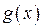нужно выбирать так, чтобы все КВ этой матрицы делились на 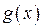без остатка. Выясним условие, при котором это возможно.

Учитывая изложенные выше правила циклического сдвига КВ, любой КВ образующей матрицы можно представить в виде:

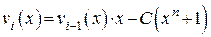, (2.28)

где C – коэффициент, принимающий значение 1, если степень 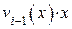равна n, и 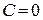, если степень 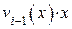меньше n; .

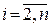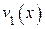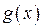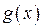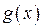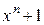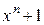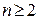Если делится на без остатка, то, как видно из (2.28), все многочлены матрицы будут делиться на без остатка только в том случае, если на будет делиться без остатка многочлен . Но многочлен при является приводимым, т.е. всегда может быть представлен в виде произведения некоторых неприводимых многочленов. Отсюда следует, что образующий многочлен 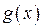должен выбираться из разложения многочлена .

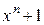Выбор конкретного образующего многочлена осуществляется в соответствии с требуемой корректирующей способностью кода.

Рассмотрим сначала случай простейшего циклического кода, обнаруживающего все одиночные ошибки.

Любая принятая комбинация 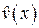, возможно, содержащая ошибку, может быть представлена в виде суммы по модулю 2 неискаженного КВ 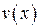и вектора ошибки , :

.

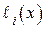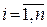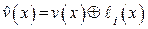Очевидно, что ошибка будет обнаружена только в том случае, если многочлен 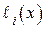, соответствующий вектору ошибки, не делится на образующий многочлен .

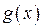Вектор одиночной ошибки имеет 1 в искаженном разряде и 0 во всех остальных разрядах, т.е. ему соответствует многочлен 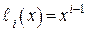. Среди неприводимых многочленов, входящих в разложение 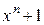и не входящих в разложение 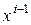, многочленом наименьшей степени является 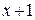. Остаток от деления любого многочлена на 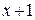представляет собой многочлен нулевой степени и может принимать только два значения: 0 или 1. Так как 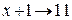, то очевидно, что при четном числе единиц в исходном КВ остаток от деления многочлена, отображающего этот КВ, на 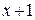будет 0, а при нечетном – 1. Следовательно, при любом числе информационных разрядов k требуется только один проверочный символ, обеспечивающий четность числа единиц в полной комбинации. Таким образом, циклический код с обнаружением одиночной ошибки является обычным кодом с проверкой на четность и способен обнаруживать не только одиночные, но и любое нечетное число ошибок.

Циклические коды с 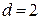не имеют практического значения. В двоичных кодах всегда проще подобрать контрольный символ 0 или 1 таким образом, чтобы сумма единиц в КВ была четной, чем строить циклический код для получения того же результата.

В случаях, когда циклический код должен не только обнаруживать, но и исправлять одиночные ошибки, выбор 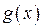осуществляется из следующих соображений. Так как информацию об искаженном разряде несет только остаток от деления векторов ошибок на образующий многочлен, то 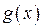должен обеспечивать требуемое число различных остатков. Но при делении любого многочлена на образующий многочлен степени m наибольшая степень остатка равна 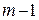, т.е. остаток содержит m разрядов. Следовательно, при двоичном кодировании и степени образующего многочлена равной m возможно получение 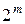различных остатков, с помощью которых нужно различить ошибку в любом из разрядов n-значной кодовой комбинации, включая и правильную передачу. Следовательно, должно выполняться условие:

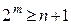(2.29)

Отсюда .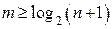

По известному m по таблицам выбирается конкретный многочлен. При этом необходимо, чтобы образующий многочлен степени m, выбранный из разложения многочлена 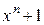, не входил бы одновременно в разложение многочлена 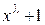, где 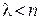, т.к. число остатков в этом случае окажется равным 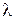. В связи с этим, после выбора конкретного многочлена, проверяют число различных остатков, для чего комбинацию в виде 1 с последующими нулями делят на образующий многочлен .

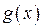Итак, для кодов с 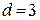образующий многочлен должен выбираться из числа неприводимых многочленов, входящих в разложение многочлена 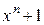, иметь степень не ниже определяемой выражением (2.29), быть по возможности более коротким, так как при этом упрощаются кодирующие и декодирующие устройства, но с числом ненулевых членов не менее заданного кодового расстояния кода.