ДРОБНО–РАЦИОНАЛЬНЫЕ ПРИБЛИЖЕНИЯ

Некоторые функции нельзя с достаточной точностью приблизить полиномами. Кроме того, полиномиальное приближение может очень медленно сходиться. В таких случаях используется дробно-рациональное приближение функции – в виде отношения двух многочленов.

Рассмотрим снова разложение функции в ряд Тейлора:

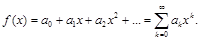
Представим эту функцию в виде отношения двух полиномов:

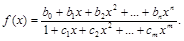
Равенство единице первого члена полинома в знаменателе не нарушает общности выражения, т.к. любое другое число можно превратить в 1, поделив на него числитель и знаменатель.

Возникает задача – определить коэффициенты b_k и с_k, считая известными коэффициенты a_k. Для этого необходимо n+1+m уравнений и столько же членов ряда Тейлора:

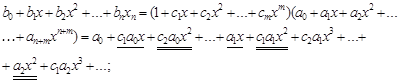Раскрывая скобки и приравнивая коэффициенты при одинаковых степенях х, получаем:

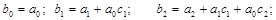
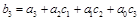и так далее.

Решая эту систему линейных алгебраических уравнений, получаем b_k и с_k .

Пример.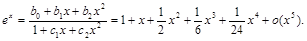

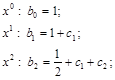
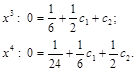
Решая систему, находим:

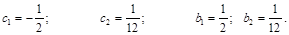
Следовательно,

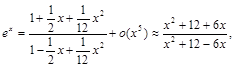
то есть это приближение по точности равносильно аппроксимации рядом Тейлора с учетом членов до 4–ого порядка включительно.

Отметим, что для расчета по ряду Тейлора (с использованием схемы Горнера) необходимо 2n=8 действий (4 умножения и 4 сложения), а для дробно–рационального приближения – 6 действий (3 умножения и деления и 3 сложения и вычитания).

Кстати, можно еще сократить количество вычислений, представив дробно–рациональное выражение в виде цепной дроби:

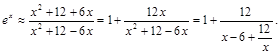
Здесь процесс вычисления осуществляется за 5 действий.