Билет № 15. Билет №15. Многочлены от одной переменной. Делимость многочлена на двучлен

Определение 5.1. Пусть дано произвольное поле F, x – переменная. Многочленом n - й степени от одной переменной называют выражение вида: a_n × xⁿ + …+ a₁× x + a₀, где a_i F (i = 0, 1, 2, …, n), a_n 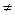0 , n Î NÈ {0}.

Замечание. a_i хⁱ называют членом многочлена; i – степенью этого члена (если a_i 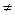0); a_i – коэффициент соответствующего члена. Если a_i = 0, то члену a_i × xⁱ не приписывается никакой степени, a₀ × x⁰ – член нулевой степени, если a_i 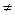0 – элемент поля F.

Многочлены от одной переменной обозначают так: f(x), g(x), h(x) и т.п.

Определение 5.2.Степенью многочлена f(x) называют наивысшую из степеней его членов (и обозначают deg f(x)).

Многочлен f(x) = 0 · хⁿ + 0 · x^n-1 + … + 0 называют нуль-многочленом. Его степень не определяется.

Множество многочленов F[x] = {f(x)| f(x) = a_n × xⁿ + …+ a₁× x + a₀} можно разбить на три класса:

1) нуль-многочлен f(x) = 0 · хⁿ + 0 · x^n-1 + … + 0;

2) многочлены нулевой степени (a_i F);

3) многочлены степени выше нулевой f(x) и g(x), …

Если даны два многочлена f(x) и g(x), то всегда можно считать, что они содержат одинаковое число членов, т.к. недостающие члены всегда можно приписать с нулевыми коэффициентами.

Определение 5.3. f(x), g(x) F [x], если

f(x) = a_n xⁿ + a_n-1 x^n-1 + … + a₁ x + a₀ и

g(x) = b_n xⁿ + b_n-1 x^n-1 + …+ b₁ x+ b₀, то

f(x) = g(x) 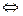(a_n = b_n ) (a_n-1 = b_n-1) … (a₀ = b₀ ).

Определим на множестве F [x] три операции:

1. f(x), g(x) F [x], f(x) + g(x) = (a_n + b_n) xⁿ +( a_n-1 + b_n-1 ) x^n-1 + …+ (a₁ +b₁) x+ +(a₀ + b₀);

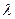
2. f(x) F [x], F , 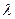f(x) = 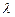a_n xⁿ +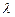a_n-1 x^n-1 + … + 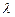a₁ x +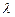a₀;

3. f(x), g(x) F [x], f(x) · g(x) = a₀ b₀ + (a₀ b₁ + a₁ b₀) х + …+ (a₀ b_i +…+ a₁ b_i-1 + + … + a_i b₀ ) xⁱ + … + a_n b_m ) x^n+m;

Теорема 5.1 (о кольце многочленов от одного переменного).

Алгебра (F[x], + , ×) является коммутативным кольцом с единицей без делителей нуля, содержащим в качестве подкольца, поле F.