Теорема 5.2 (о делении с остатком многочленов над полем).

f(x), (x)ÎF[x], (x) ¹ 0, 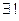q(x), r(x) F [x] : (1) f(x) = (x)× q(x) + r(x), причем deg(r(x)) < deg( (х)) или r(x) = 0.

Замечание.Равенство (1) называется равенством деления с остатком, f(x) называют делимым, (x) – делителем, q(x) – неполным частным, r(x) – остатком.

Следствие 5.3 (о делении на двучлен).Любой многочлен f(x)ÎF[x] однозначно делится с остатком на двучлен x – а, где аÎ F :

f(x) = (x – а) × q(x) + r, где r Î F.

Определение 5.4.Элемент а F называют корнем многочлена f(x), если f(а) = 0.

Следствие 5.4.f(а) = 0 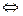f(x) 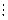(х – а).

Доказательство.

Необходимость. Пусть f(а) = 0. Докажем, что f(x) делится на (х – а). Разделим f(x) на (х – а) с остатком, получим) f(x) = (x - а) × q(x) + r, та как f(a) = 0 по условию, то 0 = 0 + r, Следовательно, r = 0, т.е. f(x) 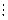(x - а).

Достаточность. Пусть f(x) 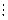(x - а), докажем, что f(а) = 0. Разделим f(x)на (x - а), получим: f(x) = (x - а) × q(x) + 0,подставим а, получим:

f(а) = (а - а) × q(а) + 0 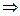f(а) = 0.

Замечание.Если f(x) делится на (х – а)^k , но f(x) не делится на (х – а)^k+1, тогда а называют корнем кратности k.

Следствие 5.5 (теорема Безу)Остаток r от деления многочлена f(x)ÎF[x] на двучлен (х – а), (а F) равен значению многочлена в точке а, т.е. r = f(а)ÎF .

Доказательство.

Действительно: f(x) = (x – а) × q(x) + r , тогда f(а) = r.