Влияние аналогового интегратора на корни характеристического уравнения

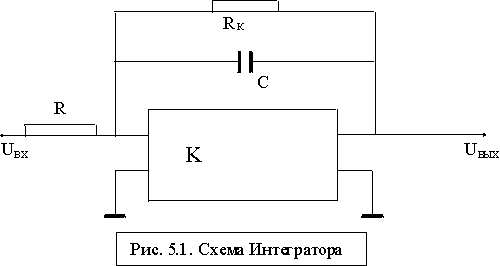
Структурная схема аналогового интегратора представлена на рис.1.

Примерные значения параметров схемы [2.9]: коэффициент усиления операционного усилителя К = 108, входное сопротивление R = 1 Мом, емкость конденсатора С = 1мф, сопротивление утечки конденсатора Rk= 10000 Мом. Передаточную функцию Wa(p) схемы можно привести к следующему виду:

Wa(p) = Ka/(p + a) ; Ka = RC = 1сек ; a = 10-41/сек

С учетом инерционных свойств операционного усилителя, передаточную функцию Wa(p) аналогового интегратора примем:

Wa(p) = 1 /(p + a)(1+Tp) ; T = 10-4сек (2.2.9)

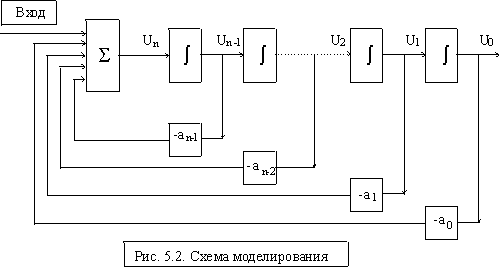
Структурная схема моделирования уравнения (1) представлена на рис.2.

Напряжения Uk, k = 0…n моделируют производные x(k) . При идеальных интеграторах с передаточной фикцией

Wи(p) = 1/p (2.2.10)

передаточная функция структурной схемы рис.5.2 имеет вид

W(p) = 1/( pn+ an-1pn-1+ an-2pn-2+…+ a1p + a0) , (2.2.11)

что соответствует уравнению (1).

Характеристическое уравнение имеет форму (2), а при известных корнях – форму (3). При наличии в уравнении (3) m вещественных корней и (n-m)/2 комплексных корней, его можно привести к виду:

P(p) = Пк=1(n-m)/2(p2+2gkp+dk2)Пi=1m(p+qi) = 0 (2.2.12)

Определение корней уравнения (12) сводится к приравниванию нулю каждого из сомножителей. Апериодическим составляющим переходного процесса соответствуют сомножители (моды) с вещественными корнями:

(p+qi) = 0 , pi= - qi, i = 1…m (2.2.13)

Колебательным составляющим переходного процесса соответствуют сомножители (моды) с комплексными корнями:

(p2+2gkp+dk2) = 0 , p1k,2k = -gk ,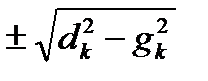

k = 1…(n – m)/2 (2.2.14)

Рассмотрим теперь работу схемы на рис.2. при аналоговых интеграторах с передаточной функцией (9), которую представим в следующем виде:

Wa(p) = 1/D(p), D(p) = (p+a)(Tp+1) (2.2.15)

Здесь D(p) – оператор аналогового интегратора.

Сравнивая передаточные функции идеального (10) и аналогового (15) интеграторов, можно видеть, что передаточную функцию схемы моделирования рис.2.2. при аналоговых интеграторах можно получить, подставив в (11) вместо оператора p из (10) оператор D из (15):

W(p) = 1/( Dn+ an-1Dn-1+ an-2Dn-2+…+ a1D + a0)

(2.2.16)

Характеристическое уравнение (12), соотношения (13) и (14) для аналоговых интеграторов также формируются путем замены p на D. Для вещественных корней, из (13)

(D + qi) = (p + a )(Tp + 1) + qi= 0 (2.2.17)

Отсюда, при малых a и T, получим:

pi1= - qi– a = pi– a ; pi2= - 1/T + qi; i = 1…m (2.2.18)

Из выражения (18) видно, что каждому вещественному корню рiхарактеристического уравнения (2) исходного уравнения соответствуют два корня схемы моделирования (рис.2.2) с аналоговыми интеграторами. Один из них – pi1– смещенный на малую величину а корень pi. Второй, дополнительный, корень pi2– располагается вблизи большой по модулю величины – 1/T .

Для комплексных корней (14), используя (15), получим уравнение четвертой степени:

(D2+2gkD+dk2) = p4+ 2p3T(1+aT) + p2(1+ 4aT+a2T2+2gkT) + 2p(1+aT)(a+gk) + (dk2+ 2gka + a2) = 0 (2.2.19)

Проектируем приближенное (для малых a и T) решение уравнения (19) ввиде:

(p2+ 2gkp + dk2)(T2p2+ 2Tzkp +1) = 0 (2.2.20)

Приравняв коэффициенты при одинаковых степенях p в уравнениях (19) и (20), можно получить приближенные соотношения:

gk2= gk2+ 2dka ; dk= dk+(a – gk2T)

zk= 1 – T(dk+a) (2.2.21)

Из выражений (20) и (21) можно видеть, что аналоговые интеграторы приводят к смещению основных комплексных корней (параметры gkи dk) , и к появлению пары дополнительных комплексных корней с вещественной частью, близкой к –1/T и затуханием zk,близким к единице.

Итак, применение аналоговых интеграторов для решения дифференциальных уравнений приводит к смещениию корней характеристического уравнения и появлению дополнительных корней.

Мерой пригодности аналоговых интеграторов для решения конкретной задачи является малость смещения основных корней и достаточно большая удаленность дополнительных корней от мнимой оси комплексной плоскости в сторону отрицательных значений. Для определенного типа аналоговой модели (с известными a и T) класс решаемых задач задается ограничениями на корни характеристического уравнения:

1/T>>[Re(pk)] >>a ; 1/T>>[Im(pk)] >>a