Нормальное (гауссовское) распределение
Это распределение занимает центральное место в теории и практике вероятностно-статистических исследований. В качестве непрерывной аппроксимации к биномиальному распределению оно впервые рассматривалось А. Муавром еще в 1733 году. Некоторое время спустя нормальное распределение было снова открыто и изучено независимо друг от друга К. Гауссом (1809 г.) и П. Лапласом (1813 г.). Оба ученых пришли к нормальному закону в связи со своей работой по теории ошибок наблюдений. Идея их объяснения механизма формирования нормально распределенных случайных величин заключается в следующем. Постулируется, что значения исследуемой непрерывной случайной величины формируются под воздействием очень большого числа независимых случайных факторов, причем сила воздействия каждого отдельного фактора мала и не может превалировать среди остальных, а характер воздействия – аддитивный. Можно показать, что функция плотности распределения случайных величин подобного типа имеет вид
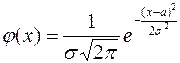 , (3)
, (3)
где 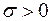 , а – любое действительное число. Само распределение называют нормальным. Проведя исследование функции
, а – любое действительное число. Само распределение называют нормальным. Проведя исследование функции 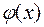 методами дифференциального исчисления, легко убедиться, что её график имеет вид:
методами дифференциального исчисления, легко убедиться, что её график имеет вид:
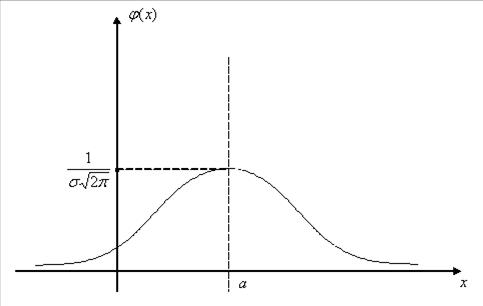
Рис. 7.1. график функции плотности нормального распределения
Найдем функцию нормального распределения. Запишем по определению (формула (2)):
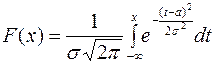 .
.
Выполним замену переменной интегрирования по формуле
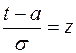 ,
, 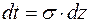 .
.
Тогда интеграл примет вид:
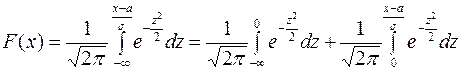 .
.
Первый интеграл в полученной формуле есть интеграл Пуассона и равен
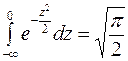 ,
,
второй интеграл – значение интегральной функции Лапласа в точке 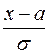 :
:
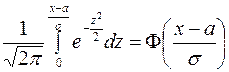 .
.
Тогда
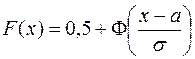 (4)
(4)
Как следствие из формулы (4) отметим следующие формулы:

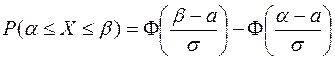 (5)
(5)
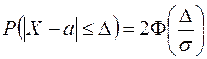 (6)
(6)
В частности, если 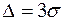 , то из формулы (6) следует
, то из формулы (6) следует
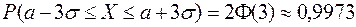 (7)
(7)
Формулу (7) часто называют «Правилом трех сигм», которое означает, что с достаточно большой вероятностью P = 0,9973, можно утверждать, что почти все значения случайной величины находятся в интервале с центром М(Х) = а и радиусом 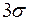 .
.
Дата добавления: 2021-12-14; просмотров: 582;











