Закон больших чисел. Теорема Чебышева.
Центральная предельная теорема
Опыт подсказывает, что события, вероятность наступления которых мала, очень редко происходят, и наоборот, события, вероятность которых близка к единице, обязательно происходят.
В связи с этим имеет место следующий принцип практической уверенности: Если вероятность некоторого события мала, то в практической деятельности поступают так, будто это событие невозможно. И событие считают достоверным, если вероятность его наступления велика.
Однако невозможно вывести математические границы этих вероятностей. Эти границы определяются статистически. Вероятность, ниже которой событие можно принять как невозможное, принято называть уровнем значимости. В статистике приняты уровни значимости 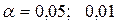 и т.д. Соответственно верхняя граница степени уверенности
и т.д. Соответственно верхняя граница степени уверенности 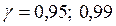 и т.д.
и т.д.
Таким образом, очень важной задачей теории вероятности является установлением закономерностей, происходящих с вероятностью близкой к единице. Всякое предложение, устанавливающее эти закономерности, называется законом больших чисел. По определению профессора А. Я. Хинчина, законом больших чисел называют общий принцип, в силу которого совокупное действие большого числа факторов приводит при некоторых, весьма общих условиях к результату, почти независящему от случая.
Некоторые конкретные условия, при которых выполняется закон больших чисел, указаны в теоремах Чебышева, Бернулли, Пуассона и Ляпунова.
Лемма Маркова
Пусть случайная величина Х принимает неотрицательные значения, A > 0 – любое число. Тогда вероятность того, что случайная величина примет значение большее чем число А, не превосходит дроби , в числителе которой стоит математическое ожидание случайной величины Х, а в знаменателе число А:
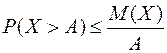
Доказательство проведем для случая дискретной случайной величины. Допустим, она принимает неотрицательные значения и имеет конечное распределение
Х 
| x1 | x2 | ... | xn |
| Р | p1 | p2 | ... | pn |
Разобьем множество всех значений на два класса. В первый отнесем значения не превышающие числа А, во второй класс – значения большие чем число А. Пусть это будут значения
{ x1, x2, … , xk } и {xk+1, xk+2, … , xn }.
Тогда
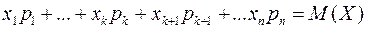
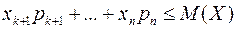
Учитывая выбор классов, получим
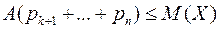
В скобках стоит сумма вероятностей тех значений случайной величины Х, которые больше числа А. Тогда
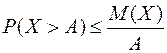 .
.
Дата добавления: 2021-12-14; просмотров: 575;











