Лекция 7. Непрерывная случайная величина и её распределения

Уточним определение непрерывной случайной величины.

Случайную величину Х назовем непрерывной, если её интегральная функция распределения непрерывна.

Класс непрерывных случайных величин, функции распределения которых всюду непрерывны и дифференцируемы, имеет и другую, удобную форму задания распределения, с помощью, так называемой функции плотности вероятности f(x), определяемой как предел

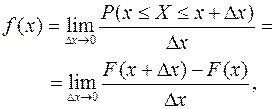
Или, что то же самое,

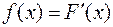(1)

Из определения и свойств функции распределения следует

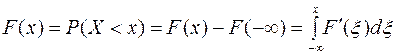
С учетом формулы (1), получим

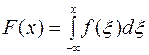(2)

В связи с введенными формулами, F(x) и f(x) получили названия интегральной и дифференциальной функций распределения соответственно.

Отметим один интересный факт: вероятность того, что непрерывная случайная величина примет какое-либо конкретное значение Х = а равна нулю:

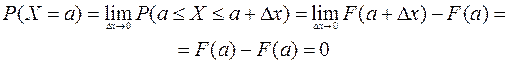
Свойства функции плотности:

1. 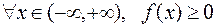. Это свойство следует из того, F(x)-неубывающая функция.

2. ,

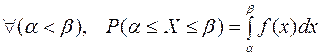3. 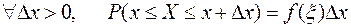. Это свойство следует из формулы Лагранжа для функции F(x).

В частности при малых значениях 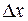, приближенно выполняется равенство

.

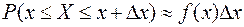4. .

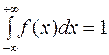Прокомментируем некоторые из этих свойств функции плотности:

Свойство 3) позволяет пояснить вероятностный смысл функции плотности. Так, предположив для определенности область возможных значений 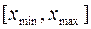случайной величины Х конечной и разбив её на одинаковые, достаточно малые интервалы группирования 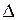с центрами в точках

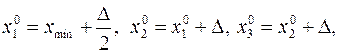и т.д.,

мы можем поставить в соответствие каждому i-му интервалу вероятность события

,

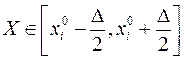равную величине 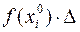. Таким образом, значения функции f(x) пропорциональны вероятности того, что исследуемая случайная величина примет значения в непосредственной близости от точки х. Отсюда следует, что наиболее вероятным (модальным) значением случайной величины является такое значение 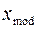, в котором функция плотности достигает своего максимума, т.е.

.

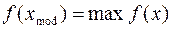Геометрическая интерпретация свойства 2) непосредственно следует из геометрического смысла определенного интеграла.