Свойства математического ожидания дискретной случайной величины
1. M(C) = C
2. M(kX) = kM(X)
3. M(X+Y) = M(X)+M(Y)
4. M(X – Y) = M(X) – M(Y)
5. Если X и Y независимые случайные величины, то
M(XY) = M(X)M(Y)
6. M(X – C) = M(X) – C , в частности M(X – M(X)) = 0
Докажем для примера свойство 3) в предположении независимости случайных величин X и Y:
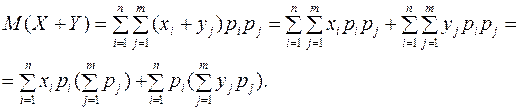
Учитывая, что
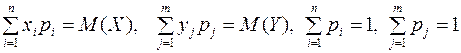
получим
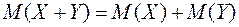 .
.
Математическое ожидание характеризует среднее ожидаемое значение случайной величины. Однако часто интересует вопрос об отклонении случайной величины от среднего значения. Такой характеристикой является дисперсия.
Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от своего математического ожидания. Формула дисперсии имеет вид:
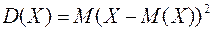
Для дискретной случайной величины формула дисперсии имеет вид:
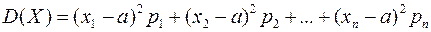 ,
,
где 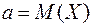 .
.
Если случайная величина Х имеет размерность, то оценивать отклонение такой величины логичнее в той же размерности. С этой целью вводят понятие среднего квадратического отклонения, как
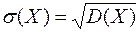
Отметим свойства дисперсии без доказательства.
1. Дисперсия постоянной величины равна нулю.
2. 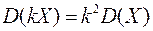
3. Если случайные величины X и Y независимы, то
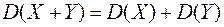
4. Для любых случайных величин справедливо равенство
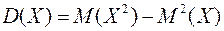
Для дискретной случайной величины последнее равенство можно записать в виде
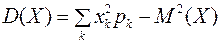
Дата добавления: 2021-12-14; просмотров: 527;











