Математическое ожидание и дисперсия некоторых случайных величин
Из перечисленных свойств легко следуют утверждения.
Теорема 1. Пусть 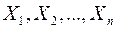 - независимые случайные величины, имеющие одинаковые математические ожидания. Тогда, математическое ожидание суммы и средней арифметической этих величин соответственно равны
- независимые случайные величины, имеющие одинаковые математические ожидания. Тогда, математическое ожидание суммы и средней арифметической этих величин соответственно равны
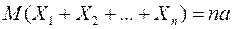 , где
, где 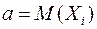 , (1)
, (1)
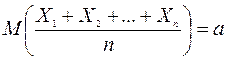 . (2)
. (2)
Теорема 2. Если 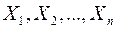 - независимые случайные величины и имеют одинаковые дисперсии, равные
- независимые случайные величины и имеют одинаковые дисперсии, равные 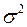 , то дисперсии суммы и средней арифметической этих величин равны соответственно
, то дисперсии суммы и средней арифметической этих величин равны соответственно
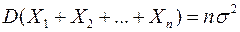 , (3)
, (3)
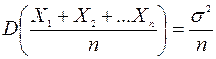 . (4)
. (4)
Теорема 3. Если Х – число наступлений события А в n независимых испытаниях, в каждом из которых оно наступает с постоянной вероятностью p (p не мало), то математическое ожидание и дисперсия случайной величины Х соответственно равны
 . (5)
. (5)
Доказательство: Пусть 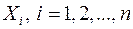 - число появления события А в каждом испытании. Очевидно, эти случайные величины не зависимы и имеют одинаковое распределение
- число появления события А в каждом испытании. Очевидно, эти случайные величины не зависимы и имеют одинаковое распределение
| Xi | ||
| Pi | q | p |
Тогда
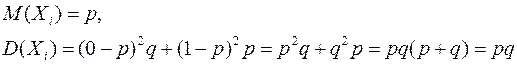
Случайную величину Х представим как сумму 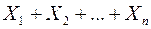 .
.
Тогда, согласно формулам (1) и (3) теорем 1,2, получим искомые равенства (5).
Теорема 4. Пусть случайная величина Х определена, так же как и в теореме 3. Назовем случайную величину Х/n – частостью события А в n независимых испытаниях. Тогда математическое ожидание и дисперсия такой случайной величины вычисляют по формулам
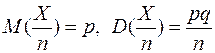
Доказательство легко следует из формул (2), (4) и теоремы 3.
Описанная в теореме случайная величина называется биномиальной или биномиально распределенной. Вероятности ее значений вычисляются по формулам Бернулли.
Если число испытаний велико, а вероятность p появления события в каждом испытании мала, то для вычисления вероятности возможного значения X = k (числа появления события) используют формулу Пуассона
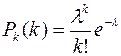 ,
,
и говорят, что случайная величина Х распределена по закону Пуассона.
Теорема 5. Математическое ожидание и дисперсия случайной величины распределенной по закону Пуассона, и принимающей счетное множество значений, равны параметру распределения 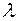 .
.
Дата добавления: 2021-12-14; просмотров: 533;











