Лекция 8. Математическое ожидание, дисперсия, моменты непрерывной случайной величины

Математическим ожиданием непрерывной случайной величины называют несобственный интеграл вида

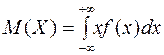(1)

Дисперсией непрерывной случайной величины называют несобственный интеграл

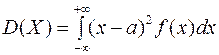, (2)

где .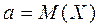

Нетрудно доказать, что

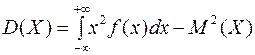(3)

Если математическое ожидание непрерывной случайной величины Х существует, то несобственный интеграл (1) сходится абсолютно. Следовательно, можно указать достаточно большое число C > 0, что для всех значений х, таких, что 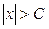, интеграл

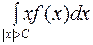
будет как угодно мал.

Таким образом, в математическом ожидании доля больших значений случайной величины незначительна. Чтобы детальнее охарактеризовать случайную величину вводят дополнительные числовые характеристики.

Начальным моментом k-го порядка называют математическое ожидание k-ой степени случайной величины Х.

Для дискретной случайной величины этот момент равен:

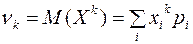(4)

Для непрерывной случайной величины:

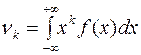(5)

Центральным моментом k-ого порядка называется математическое ожидание k-ой степени отклонения случайной величины X от своего математического ожидания M(X) = a.

В случае дискретной случайной величины:

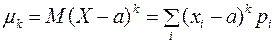(6)

Для непрерывной случайной величины:

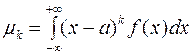(7)

С помощью свойств математического ожидания легко показать, что

(8)

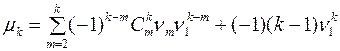(9)

В частности для первых четырёх моментов формула (9) даёт следующие равенства:

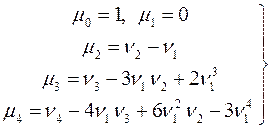(10)

Первые моменты играют важную роль в статистике при нахождении параметров распределения.