Колебательное звено.
Динамика процессов в колебательном звене описывается уравнением:
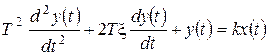 ,
,
где k - коэффициент усиления звена; Т - постоянная времени колебательного звена; 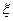 - коэффициент демпфирования звена (или коэффициент затухания).
- коэффициент демпфирования звена (или коэффициент затухания).
В зависимости от величины коэффициента демпфирования различают четыре типа звеньев:
а) колебательное 0< 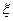 <1;
<1;
б) апериодическое звено II порядка 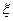 >1;
>1;
в) консервативное звено 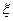 =0;
=0;
г) неустойчивое колебательное звено 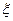 <0.
<0.
1. Переходная характеристика колебательного звена (рис. 32-35):
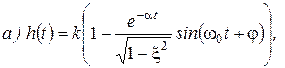
где 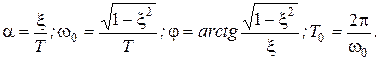
Амплитуды первых двух колебаний определяют величину 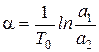 , или её можно найти, определив постоянную времени экспоненты, с которой происходит затухание
, или её можно найти, определив постоянную времени экспоненты, с которой происходит затухание 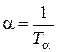 .
.
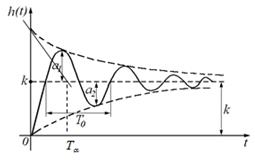
Рисунок 32
Чем ближе коэффициент затухания к единице, тем меньше амплитуда колебаний, чем меньше Т, тем быстрее устанавливаются переходные процессы.
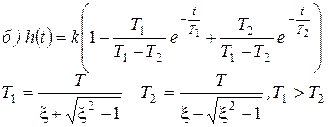
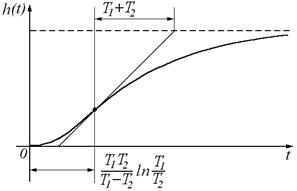
Рисунок 33
При x >1 колебательное звено называется апериодическим звеном второго порядка (последовательное соединение двух апериодических звеньев с постоянными времени Т1 и Т2).
|
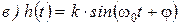 , или можно записать так
, или можно записать так 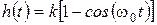 .
.
Здесь w0 – величина, обратная постоянной времени ( 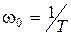 );
); 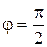 .
.
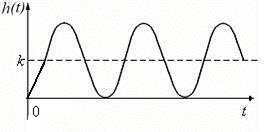
Рисунок 34
Такое звено в литературе называют консервативным звеном.
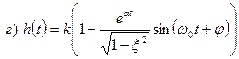
Все переходные характеристики будут колебаться вдоль величины k.
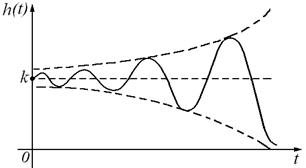
Рисунок 35
2. Импульсная переходная характеристика (рис. 36-38):
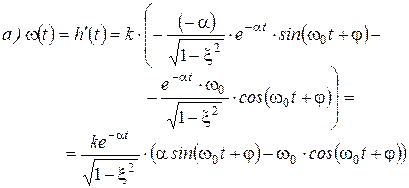
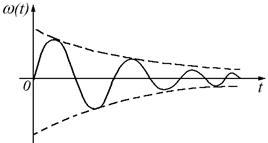
Рисунок 36
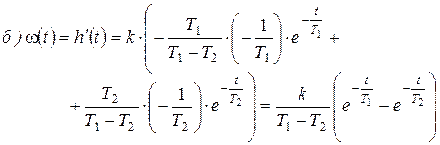
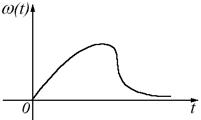
Рисунок 37
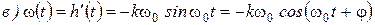 .
.
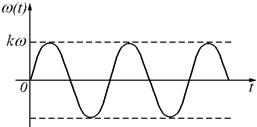
Рисунок 38
3.Передаточная функция (рис. 39):
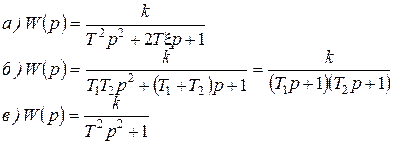
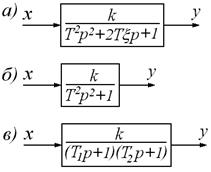
Рисунок 39
4.АФЧХ:
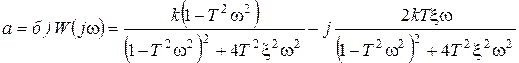
График АФЧХ будет выглядеть следующим образом (рис. 40): 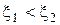
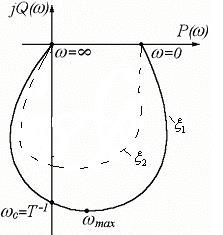
Рисунок 40
Это характеристика для колебательного звена и для апериодического звена второго порядка.
Для апериодического звена - 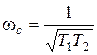 .
.
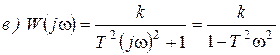 - АФЧХ для консервативного звена (рис. 41).
- АФЧХ для консервативного звена (рис. 41).
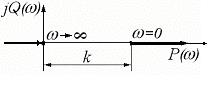
Рисунок 41
5.АЧХ:
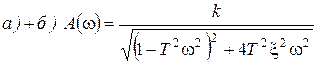 .
.
АЧХ при частоте 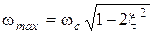 имеет максимум (резонансный пик), равный
имеет максимум (резонансный пик), равный 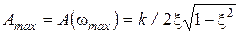 .
.
Отсюда видно, что, чем меньше коэффициент x, тем больше резонансный пик.
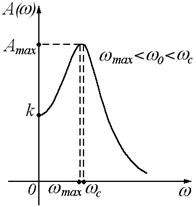
Рисунок 42 – К случаю «а»
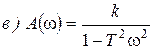
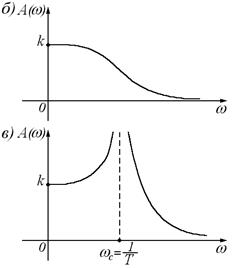
Рисунок 43 – К случаю «б» и «в»
Т.о., по графику АЧХ видно, что колебательное звено, как и все инерционные звенья, хорошо пропускает сигналы низкой частоты и плохо – сигналы высокой частоты; если частота гармонического входного сигнала близка к частоте собственных колебаний звена, то отношение амплитуды выходного сигнала к амплитуде входного больше передаточного коэффициента k.
6.ФЧХ (рис. 44, 45):
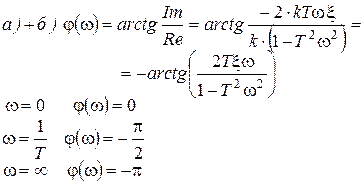
Для случая б) график будет аналогичным, только перегиб будет чуть меньше (штриховая линия на графике).
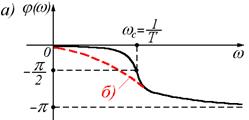
Рисунок 44 – К случаю «а»
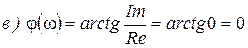
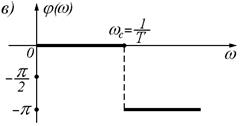
Рисунок 45
7. ЛАЧХ:
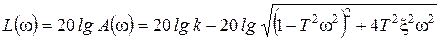 ,
,
где 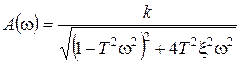 .
.
Асимптотическая ЛАЧХ колебательного звена (рис. 46, 47):
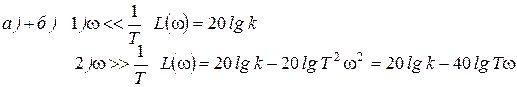
Определяем наклон на втором участке:
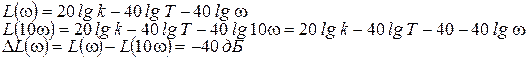
Шаблон к графику а) (рис. 47) дается от 0 до 1 шагом в 0,1.
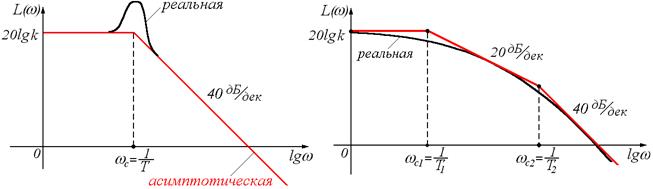
Рисунок 46 Рисунок 47
Консервативное звено (рис. 48):
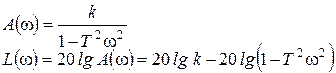
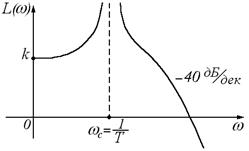
Рисунок 48
Структурная схема колебательного звена показана на рис. 49:
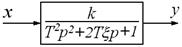
Рисунок 49
Примером колебательного звена является любая RLС- цепь (рис. 50).
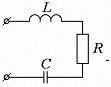
Рисунок 50
6.3 Звено запаздывания.
Примеры - конвейеры, трубопроводы.
Звеном чистого запаздывания называется такое звено, выходная величина которого полностью повторяет входную величину, но со сдвигом во времени на величину t (время запаздывания).
Динамика процесса описывается уравнением (рис. 51):
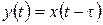 ,
,
где t - длительность запаздывания.
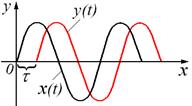
Рисунок 51
1. Переходная характеристика:
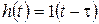
2. Импульсная переходная характеристика:
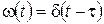
3. Передаточная функция звена:
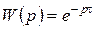
4. АФЧХ:
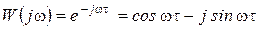
представляет собой окружность с центром в начале координат и радиусом, равным единице.
5. АЧХ:
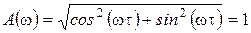
6. ФЧХ:
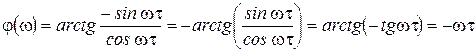
7. ЛАЧХ: 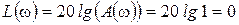 .
.
Графическая интерпретация аналитически вышеописанных характеристик звена запаздывания приведена на рис. 52.
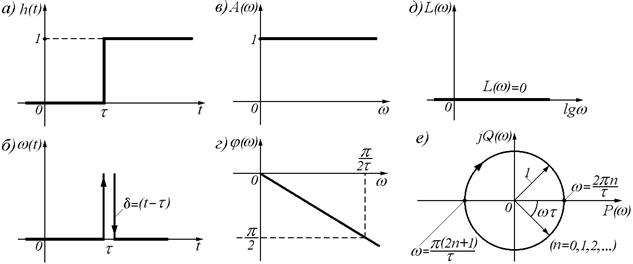
Рисунок 52
Структурная схема звена запаздывания приведена на рис. 53.
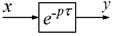
Рисунок 53
Звенья запаздывания (ЗЗ) в большинстве случаев ухудшают устойчивость систем и делают их трудноуправляемыми.
Если ЗЗ входит в контур системы, то характеристическое уравнение системы будет уже не простым, а трансцендентным. Решение и анализ трансцендентных уравнений связаны с большими трудностями  часто в практических расчетах трансцендентную передаточную функцию раскладывают в ряд Пада и, учитывая только 2 или 3 члена ряда, приближенно заменяют дробно-рациональной функцией:
часто в практических расчетах трансцендентную передаточную функцию раскладывают в ряд Пада и, учитывая только 2 или 3 члена ряда, приближенно заменяют дробно-рациональной функцией:
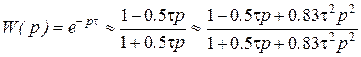 .
.
Другим возможным способом аппроксимации ЗЗ является его представление в виде последовательного соединения n инерционных звеньев первого порядка с постоянной времени 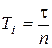 .
.
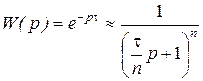 .
.
Чем больше n, тем точнее аппроксимация.
Рекомендованная литература по лекции: [1, 2].
Лекция 7 «Соединения звеньев»
7.1 Типовая схема САР.
7.2 Преобразования структурных схем. Теоремы о соединении звеньев.
7.1 Типовая схема САР
На рисунке 54 представлена обобщенная функциональная схема системы автоматического регулирования.
Устройства и элементы, входящие в автоматическую систему, имеют следующее назначение:
1 - задающее устройство преобразует управляющее воздействие в управляющий сигнал, пропорциональный заданному значению регулируемой величины. Задающими устройствами могут быть пружины, калиброванные сопротивления, грузы, уровни и т.п.
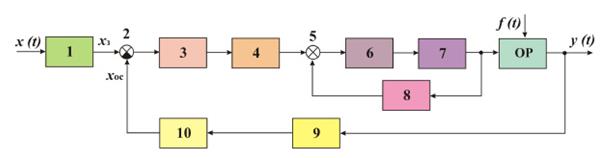
Рисунок 54 – Функциональная схема обобщенной системы
автоматического регулирования
2 - сравнивающее устройство производит сравнение двух величин с целью определения степени их рассогласования и выработки при необходимости соответствующих управляющих воздействий. Чаще всего оно представляет собой простейшее арифметическое устройство, осуществляющее вычитание из измеренного чувствительным элементом значения регулируемой величины другой величины, принятой в данном регуляторе за заданную величину.
3 - преобразующее устройство преобразует одну физическую величину в другую, более удобную для использования в процессе регулирования, не выполняя при этом функции измерения, усиления или коррекции.
4, 8 - корректирующие устройства повышают устойчивость и улучшают динамические свойства автоматической системы. В зависимости от способов включения корректирующие устройства подразделяют на последовательные или параллельные. С помощью последовательных корректирующих устройств преобразуется сигнал ошибки и в закон регулирования вводятся воздействия по производным и интегралам регулируемой величины по времени. Параллельные корректирующие устройства осуществляют подачу сигнала с выхода звена на вход одного из предыдущих для повышения устойчивости или качества регулирования.
5 - вспомогательное сравнивающее устройство сопоставляет сигнал в промежуточной точке прямой цепи с сигналом местной обратной связи.
6 - усилительное устройство предназначено для усиления мощности сигналов в регуляторах. Оно управляет энергией, которая поступает от постороннего источника энергии. В настоящее время применяют электронные и электромагнитные устройства, позволяющие использовать для действия регуляторов мощность электрической сети или специальных электрических машин; гидравлические золотники, управляющие энергией маслонапорных установок, пневматические усилители, использующие энергию сжатого воздуха и т.п.
7 - исполнительное устройство вырабатывает регулирующее воздействие, которое непосредственно прикладывается к объекту регулирования и оказывает воздействие на регулирующий орган.
9 - чувствительный элемент предназначен для точного преобразования регулируемых величин или возмущающих воздействий в сигналы управления, удобные для дальнейшего использования в процессе регулирования. Чаще всего значения регулируемых величин преобразуются в пропорциональные электрические сигналы или механические перемещения. Чувствительные элементы автоматических систем, так же как и в измерительных приборах, должны удовлетворять определенному классу точности.
10 - элемент главной обратной связи вырабатывает сигнал, находящийся в определенной функциональной зависимости от регулируемой величины.
7.2 Преобразования структурных схем. Теоремы о соединении звеньев.
Структура схема автоматической системы графически отображает ее состав, входящие в систему звенья и связи между ними.
В отличие от физических или электрических схем, где отражаются аппаратурные особенности, энергетика, физическая природа сигналов и т.п., в структурной схеме ставится задача: в наиболее наглядной форме показать математическую сторону преобразования сигналов, изменяющихся во времени, отдельными элементами и всей системой в целом.
При анализе и синтезе автоматических систем широко используется структурный анализ. Т.к. структурная схема является графическим изображением дифференциального уравнения автоматической системы и обладает главным достоинством любого графического представления - наглядностью.
Составление структурной схемы является одним из первых этапов исследования сложных объектов регулирования, она может быть составлена на основании математического описания автоматической системы, а также исходя из физической модели объекта.
Структурная схема автоматической схемы может быть задана во временной области, в которой условия преобразования сигналов описываются в общем случае дифференциальными уравнениями, и в области преобразований или изображений по Лапласу или Фурье, где справедливы алгебраические соотношения.
Наибольшее распространение получили структурные схемы линейных автоматических систем с постоянными параметрами, в которых свойства элементов задаются достаточно просто их передаточными функциями. Для систем с изменяющимися во времени параметрами математические зависимости в области временного аргумента получают графическое изображение, аналогичное системам с постоянными параметрами. Достаточно эффективен структурный переход к зависимостям в области второго временного аргумента, входящего в сопряженные дифференциальные уравнения. Эти структуры называются структурными изображениями уравнений. Существуют для переменных систем и структурные схемы в области комплексного аргумента, содержащие параметрическую передаточную функцию, преобразуемую значительно более сложно.
Для нелинейных систем вводится понятие функциональной структурной схемы, но имеется существенное ограничение в использовании структурных методов, так как принцип суперпозиции для нелинейных систем несправедлив. Область структурного анализа существенно расширяется при переходе к линеаризованным схемам. Структурные методы охватывают: правила начертания структуры системы по заданным исходным данным, способы эквивалентных преобразований структур для выявления передаточных свойств системы между характерными точками схемы при ее анализе и, наконец, рекомендации по целенаправленному изменению структуры системы при ее синтезе.
Структурные методы в применении к отдельным динамическим звеньям позволяют вскрывать их внутреннюю структуру, что способствует более ясному пониманию существа процессов, протекающих в звеньях, и позволяют правильно подойти к улучшению характеристик путем наложения дополнительных внешних связей, усиливающих благоприятные или нейтрализирующие нежелательные внутренние связи.
Применительно к системе в целом структурные методы позволяют установить рациональность системы с точки зрения решения основной возлагаемой на нее задачи по воспроизведению управляющего воздействия при одновременной компенсации действующих на систему возмущений. Структурные методы не могут быть противопоставлены в своей основе аналитическим методам линейных преобразований, но делают их более наглядными и удобными для практики. Аналогом структурных преобразований может служить метод преобразования из звезды в треугольник и обратно, широко применимый при ряде расчетов электрических цепей вместо аналитических методов контурных токов или узловых напряжений.
В задачу структурных методов не входит полное решение дифференциальных уравнений звеньев и автоматической системы в целом, но детализированная структура непосредственно используется для настройки по ней схемы автоматической системы непрерывного действия, на который могут быть получены искомые решения.
Разработка структурных методов ведется уже достаточно давно. Так была предложена специальная алгебра структурного анализа и синтеза. Разработаны элементы структурных методов применительно к задачам устойчивости и терминология в области структурных методов.
Основными типами соединений звеньев в автоматических системах являются:
- последовательное соединение;
- параллельное соединение;
- обратная связь.
Очевидно, что при любых видах соединений линейных звеньев полученная в результате соединений система будет линейной.
Последовательное соединение звеньев (рис. 55). Последовательным называется такое соединение звеньев, при котором выход каждого предыдущего связан со входом последующего звена.

Рисунок 55 – Схема последовательного соединения звеньев
При последовательном соединении n звеньев с соответствующими передаточными функциями уравнения связи в операторной форме имеют вид:
х1 = W1(p)x;
х2 = W2(p)x1;
х3 = W3(p) x2;
……………...
у = Wп(p)xп-1.
Исключив из данных уравнений все промежуточные переменные, кроме входной и выходной величин, получим
у = [W1(p) W2(p) W3(p)… Wп(p)]x.
Из этой зависимости определяем, что передаточная функция системы последовательного соединенных звеньев равна произведению передаточных функций всех звеньев, входящих в соединение. Коэффициент передачи цепи последовательно соединенных звеньев равен произведению коэффициентов передачи всех звеньев.
Комплексная передаточная функция последовательно соединенных звеньев равна произведению комплексных передаточных функций всех звеньев, входящих в соединение.
Выражение для амплитудной частотной характеристики
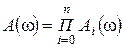
и фазовой частотной характеристики последовательного соединения звеньев
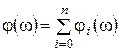 .
.
Следует подчеркнуть, что это справедливо только в том случае, если соединение выхода предыдущего звена со входом последующего не меняет исходных уравнений каждого звена и, следовательно, его передаточной функции. В подобной последовательной цепи звеньев сигнал проходит только в одном направлении.
Если при соединении двух звеньев наблюдается влияние одного звена на другое, в результате которого меняются исходные уравнения одного из звеньев, то такое соединение двух звеньев должно рассматриваться как новое самостоятельное звено со своей передаточной функцией.
Параллельное соединение (рис. 56). Параллельным (согласным) называется такое соединение звеньев, при котором входные воздействия всех звеньев одинаковы, а их реакции алгебраически суммируются
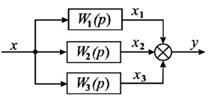
Рисунок 56 – Схема параллельного согласного соединения звеньев
При параллельном соединении n звеньев с соответствующими передаточными функциями уравнения связи в операторной форме имеют вид:
х1 = W1(p)x;
х2 = W2(p)x1;
х3 = W3(p) x2;
……………...
у = Wп(p)xп-1.
Исключив из данных уравнений все промежуточные переменные, кроме входной и выходной величин, получим
у = [W1(p) + W2(p) + W3(p) +…+ Wп(p)]x.
Из этой зависимости определяем, что передаточная функция системы параллельного (согласного) соединенных звеньев равна сумме передаточных функций всех звеньев, входящих в соединение. Коэффициент передачи цепи параллельного соединенных звеньев равен сумме коэффициентов передачи всех звеньев.
Комплексная передаточная функция параллельного соединенных звеньев равна сумме комплексных передаточных функций всех звеньев, входящих в соединение.
Параллельное соединение звеньев позволяет получить различные законы автоматического регулирования - введение интеграла, форсировкой и т.п. Построение частотных характеристик данного типа соединения звеньев связано с известными трудностями.
В данном случае также справедливо то, что если соединение звеньев не меняет исходных уравнений каждого звена и, следовательно, его передаточной функции.
Если при соединении звеньев наблюдается влияние одного звена на другое, в результате которого меняются исходные уравнения одного из звеньев, то такое соединение звеньев должно рассматриваться как новое самостоятельное звено со своей передаточной функцией.
Обратная связь (рис. 57). Обратной связью называется такое соединение звеньев, при котором часть воздействия с выхода автоматической системы (звена) передается на ее вход.
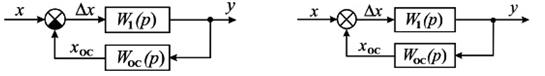
| а | б |
Рисунок 57 – Схема системы с отрицательной (а) и положительной (б) отрицательной связью
Понятие обратная связь имеет фундаментальное значение в теории автоматического регулирования. Любая автоматическая система, построенная в соответствии с принципом автоматического регулирования по отклонению, имеет основную отрицательную связь. Кроме основной обратной связи, системы могут иметь дополнительные, предназначенные для коррекции динамических свойств отдельных звеньев и системы в целом. Дополнительные обратные связи могут быть отрицательными или положительными в зависимости от их назначения.
При наличии обратной связи образуется замкнутый контур передачи воздействий от одного звена к другому. Выходной сигнал первого звена (реакция системы в целом) подается на вход звена обратной связи, который с соответствующим знаком суммируется со входным сигналом системы. В результате на вход звена подается сигнал рассогласования или суммы.
В случае отрицательной обратной связи
ΔХ=Х – ХОС.
В случае положительной обратной связи
ΔХ=Х+ХОС.
Исключив из данных уравнений все промежуточные переменные, кроме входной и выходной величин, получим.
В случае отрицательной обратной связи
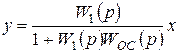 .
.
В случае положительной обратной связи
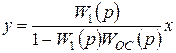
Из этих зависимостей определяем, что передаточная функция системы (звена), охваченного обратной связью, равно частному, в числителе которого стоит передаточная функция охватываемого звена, а в знаменателе - сумма (разность) единицы и произведения передаточной функции охватываемого звена на передаточную функцию звена обратной связи.
В практике автоматического регулирования чаще всего встречаются отрицательные обратные связи.
Общее выражение для комплексной передаточной функции системы с обратной связью равно частному, в числителе которого стоит комплексная передаточная функция охватываемого звена, а в знаменателе - сумма (разность) единицы и произведения комплексной передаточной функции охватываемого звена на комплексную передаточную функцию звена обратной связи.
Реальные объекты обладают сложной структурой. Упрощение вывода передаточных функций сложных объектов в схемах достигается за счет преобразования их структурных схем к трем рассмотренным основным типам соединений.
Критерий правильности преобразования структурной схемы заключается в том, чтобы входные и выходные сигналы преобразуемого участка до и после преобразования были одинаковы.
На практике редко встречаются схемы, в которых можно сразу же выделить тот или иной тип соединений, как правило, имеются, так называемые, перекрестные связи. В этом случае возникает необходимость перестановки и переноса сумматоров и узлов.
Перемещение звеньев и связей (Преобразования перекрестных структурных схем). Перекрестной будем называть структурную схему, для которой последовательное свертывание внутренних контуров на основе выведенных выше формул не может быть непосредственно проведено из-за присутствия в контурах дополнительных узлов и сумматоров. Через эти элементы данный контур обычно связан с другими контурами, или в него вводятся дополнительные входные воздействия, а также могут вводиться дополнительные реакции. Затрудняющие свертывание схемы узлы при соблюдении эквивалентности сигналов во всех входных и выходных линиях.
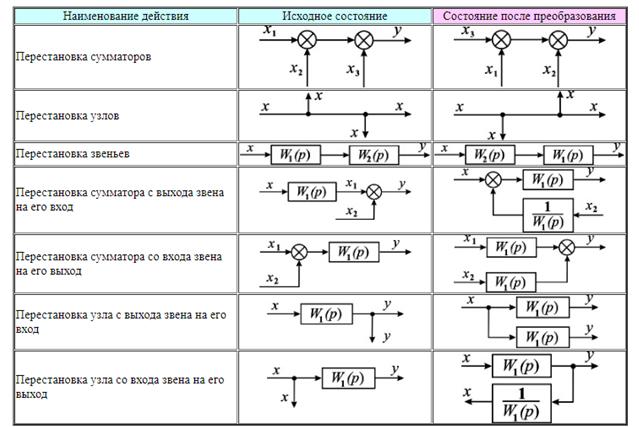
Перестановка однородных элементов. Взаимная перестановка однородных элементов обоснована свойством однонаправленности структурной схемы, согласно которому любое число ответвлений узлов не меняет величину сигнала (табл. 3).
Предварительное преобразование структурных схем является более удобным, чем составление системы дифференциальных уравнений и применять к ней преобразование Лапласа. Это преимущество заключается в том, что громоздкое формальное решение совместных уравнений заменяется наглядными преобразованиями, имеющими геометрическую интерпретацию и уменьшающими возможность ошибки.
Таким образом, в результате анализа и структурных преобразований возможно упрощение сложных схема автоматического регулирования, получение уравнения автоматической системы, исследование статических характеристик и выработка практических рекомендаций, направленных на повышение качества регулирования.
Таблица 3 – Правила перестановки однотипных элементов
При наличии нелинейных статических характеристик отдельных звеньев автоматической системы (например, объекта или регулятора, это характерно для элементов автоматики) анализ производится с использованием метода линейно-кусочной аппроксимации, т.е. реальную характеристику на отдельных участках заменяют прямолинейной статической характеристикой.
Рекомендованная литература по лекции: [1].
Лекция 8 «Уравнения динамики и статики типовой САР»
8.1 Основные понятия и показатели качества.
8.2 Анализ качества процессов.
В общем случае звенья (рис. 58) и системы описывают нелинейными дифференциальными уравнениями произвольного порядка.

Рисунок 58
Звено можно описать дифференциальным уравнением второго порядка
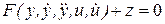 ,
,
где y – выходная величина,
u, z- входные величины,
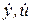 - первые производные по времени,
- первые производные по времени,
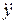 - вторая производная по времени.
- вторая производная по времени.
Это уравнение, описывающее процессы в звене при произвольных входных воздействиях, называется уравнением динамики.
Пусть при постоянных входных величинах u=u0 и z=z0 процесс в звене с течением времени установится: выходная величина y=y0. Тогда уравнение примет вид
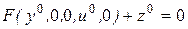 .
.
Это уравнение описывает статический (установившийся) режим, его называют уравнением статики.
Статический режим можно описать графически.
Статическая характеристика – это зависимость выходной величины от входной в статическом режиме (воздействие u и возмущение z постоянны во времени, тогда управляемая величина Y = f(U,Z)).
8.1 Анализ качества процессов.
Качество автоматической системы управления определяется совокупностью свойств, обеспечивающих эффективное функционирование как самого объекта управления, так и управляющего устройства, т.е. всей системы управления в целом.
Свойства, составляющие эту совокупность и имеющие количественные измерители, называются показателями качества системы управления.
Качество автоматической системы, как и любого технического устройчства, может быть оценено такими общепринятыми показателями, как вес системы, её габариты, стоимость, надёжность, долговечность и т.п. Совокупность этих общетехнических показателей характеризует качество СУ в широком смысле.
В ТАУ и в практике автоматизации термины «качество системы», «качество управления» используют, как правило, в более узком смысле: рассматривают только статические и динамические свойства системы. Эти свойства предопределяют точность поддержания управляемой величины (выходной величины объекта) на заданном уровне в установившихся и переходных режимах, т.е. обеспечивают эффективность процесса управления. Для такого, более узкого понятия качества САУ, охватывающего только её статические и динамические свойства, применяют термин «качество управления», а сами свойства системы, выраженные в количественной форме, называют показателями качества управления.
Для анализа качества управления могут быть использованы прямые и косвенные методы оценки. Прямые методы определения качества базируются на исследовании переходного процесса, дают наиболее достоверную информацию с последующим определением показаний качества. Косвенные методы определения качества позволяют по косвенным признакам, не решая ни дифференциальных, ни характеристических уравнений, получить приближенный переходный процесс с приближенными показателями качества. К особой категории показателей качества относятся интегральные оценки, которые вычисляют либо непосредственно по переходной функции системы, либо по коэффициентам передаточной функции системы.
8.2 Основные понятия и показатели качества.
1. Качество САУ определяется следующими показателями (рис. 59):
Время достижения установившегося режима, время переходного процесса, время регулирования – 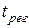 - такое время, по истечении которого для управляемой величины выполняется условие:
- такое время, по истечении которого для управляемой величины выполняется условие:
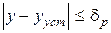 ,
,
где у – управляемая величина; dр – некоторая величина (для САУ 5% от установившегося режима).
2. Перерегулирование - это процентное соотношение разницы максимального перерегулирования и установившегося значения:
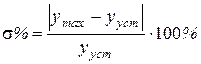 .
.
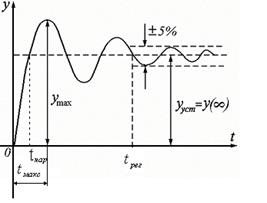
Рисунок 59
3. Время достижения первого максимума (tмакс), такое время, при котором выходная величина достигает своего максимального по модулю значения:
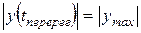 .
.
4. Время нарастания – tнар
5. Число перерегулирований – это количество раз, когда управляемая величина превышает по модулю значение:
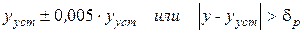 .
.
6. Частота колебаний 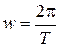 , где Т – период колебаний
, где Т – период колебаний
7. Ошибка в установившемся режиме (характеризует точность САУ)
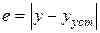 .
.
Помимо этих показателей, могут рассматриваться ещё некоторые другие, например, в качестве показателя может быть взята величина 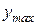 , или рассчитана величина декремента затухания
, или рассчитана величина декремента затухания 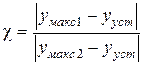 и т.д.
и т.д.
Первые показатели – это показатели качества переходного процесса, а последний – показатель качества в установившемся режиме
Рекомендованная литература по лекции: [1, 2].
Лекция 9 «Частотные оценки качества»
9.1 Оценка качества по распределению полюсов и нулей передаточной функции.
9.2 Интегральные оценки качества.
9.1 Оценка качества по распределению полюсов и нулей передаточной функции.
Дата добавления: 2018-11-26; просмотров: 4008;











