Колебательное звено

Дифференциальные уравнение такое же как и у апериодического второго порядка, однако, корни характеристического

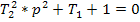(83)

Уравнение (83) комплексно сопряженные при условии ,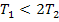

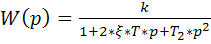(84)

Или 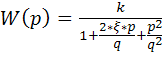(84’)

(84) – передаточная функция

(84’) – где 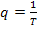- угловая частота свободы колебаний при отсутствии затухания

ξ – параметр затухания

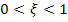обозначим ω = 1/T

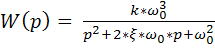(84’’)

Пример 1.

К колебательным звеньям второго порядка можно отнести RLC – цепи

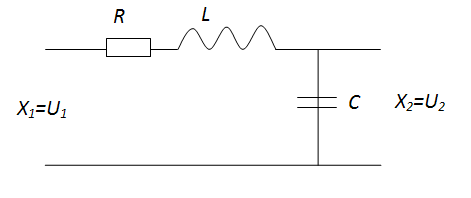
Дифференциальное уравнение

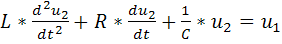(85)

, , , -

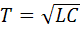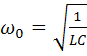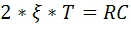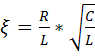Коэффициент затухания или декремент затухания.

Пример 2.

Управляемые двигатели постоянного тока, для которых выполняется условие

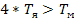
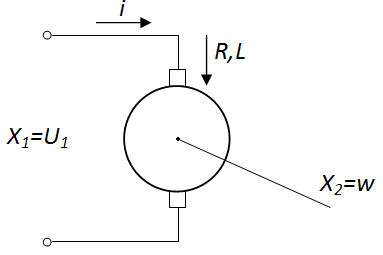R, L – параметры обмотки двигателя

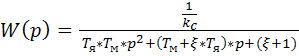(86)

, где 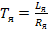; 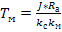- механическая постоянная времени

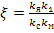– коэффициент

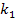- коэффициент пропорциональности находится из выражения

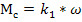- статический момент на двигателе

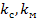- коэффициенты пропорциональности

,

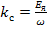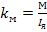
М – момент развивающий двигатель

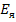- противо ЭДС

Передаточная функция по углу для такого двигателя

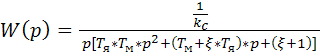(87)

Пример 3.

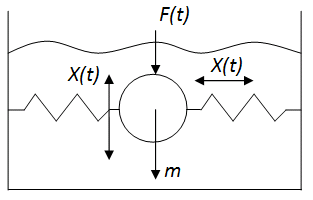
Упругие механические системы включающие элементы конечной жесткости. (пружины, элементы с трением (вязкое трение и т.д. ) элементы с конечными массами).

например 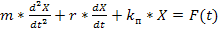, где

r – Коэффициент вязкого трения

m – Перемещающаяся масса

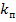- жесткость пружины

F(t) – сила приложенная к телу

Уравнение описывает движение тела в жидкости с центровками его пружины

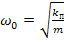– свободная частота

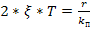, - коэффициент затухания