Влияние нулей передаточной функции на качество переходного процесса.

Корни знаменателя называются корнями характеристического уравнения или полюсами передаточной функции. Корни числителя называются нулями передаточной функции. Чтобы исследовать САУ на устойчивость и на качество управления необходимо определить нули и полюса передаточной функции. Перед исследованием нужно проверить: 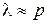. Если 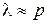, то их нужно сократить, и они не будут влиять ни на качество, ни на устойчивость.

Рассмотрим частный случай, когда передаточная функция системы имеет вид:

,

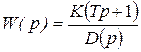где 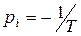- ноль передаточной функции.

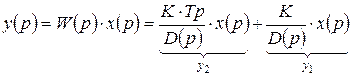
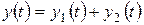- переходный процесс y(t) состоит из двух составляющих, при этом:

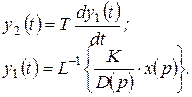
Графически (рис. 61) это означает, что если просуммировать y₁(t) и y₂(t), то получим верхний график y(t).

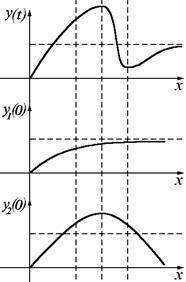
Рисунок 61

Т.о. нули передаточной функции не увеличивают время переходного процесса, а вносят колебательность в переходный процесс. Нули передаточной функции не влияют на устойчивость системы, поэтому при синтезе линейных САУ, отвечающих максимальному быстродействию, можно не рассматривать нули передаточной функции.

Рассмотрим случай, когда ноль передаточной функции совпадает с полюсом.

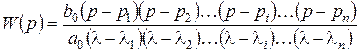
Будем считать, что 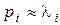, это означает следующее.

Если l_i была величина положительная и единственная, то полюс p_i скомпенсировал данный корень и САУ будет устойчивой. Т.о., компенсация нулей передаточной функции и полюсов передаточной функции может быть использована в построении корректирующих устройств САУ.

9.2 Интегральные оценки качества.

Каждый из рассмотренных выше прямых и косвенных показателей качества характеризует лишь одно какое-либо свойство системы, лишь один признак ПП или частотной характеристики. Причём, все показатели качества связаны с настроечными параметрами регулятора сложными зависимостями, имеющими, как правило, противоречивый характер: изменение параметра приводит к улучшения одних показателей качества и к ухудшению других. Это значительно усложняет выбор параметров регулятора. Поэтому в инженерной практике широко используются интегральные показатели качества.

Интегральные оценки представляют собой определенные интегралы по времени (в пределах от 0 до 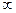, или до ожидаемого времени переходного процесса) от некоторой функции управляемой переменной y(t) (или сигнала ошибки e(t)): .

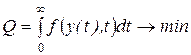Подынтегральная функция f выбирается таким образом, чтобы интеграл лучше характеризовал качество системы и проще выражался через коэффициенты передаточной функции замкнутой системы. Чтобы интеграл был сходящимся, в функцию f вводят не абсолютные значения y(t) или e(t), а их отклонения от конечных, установившихся значений.

Линейная интегральная оценка.

Простейшей интегральной оценкой является линейная интегральная оценка

,

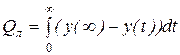которая равна площади (рис. 62), заключённой между прямой 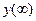и кривой ПП.

Интегральная оценка учитывает как величину динамических отклонений, так и длительность их существования. Поэтому, чем меньше оценка (область S), тем лучше качество процессов управления, тем быстрее заканчивается ПП, тем меньше отклонение сигнала y(t) от y_з.

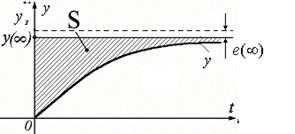
Рисунок 62

Разность под знаком интеграла равна динамической или переходной составляющей сигнала ошибки:

.

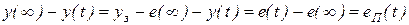Поэтому линейную интегральную оценку чаще определяют в таком виде:

.

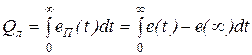Метод Кулебакина.

.

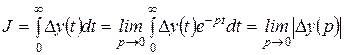Рассмотрим следующую передаточную функцию:

.

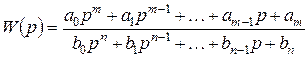В качестве входного сигнала x(t) рассмотрим ступенчатое воздействие r(t).

,

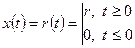тогда 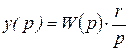, а .

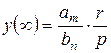Интегральная схема будет выглядеть так:

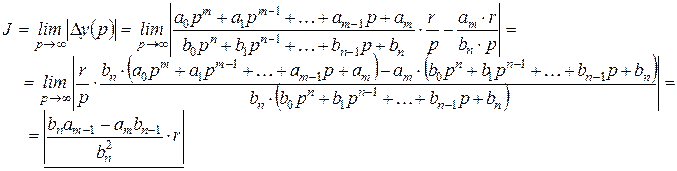Если рассматривать минимум этой функции, то он будет достигаться при выполнении равенства

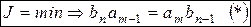
это идеальный переходный процесс (площадь S – min).

Т.о. выбирая коэффициенты передаточной функции в соответствии с равенством (*), можно достичь заданных показателей качества.

Модульная интегральная оценка (рис. 63).

Но недостатком линейной интегральной оценки является то, что её можно применять только для монотонных (апериодических) переходных процессов.

Интеграл, вычисленный для знакопеременной кривой 1 , будет существенно меньше интеграла, вычисленного для апериодической кривой 2, хотя качество ПП для кривой 2 явно лучше.

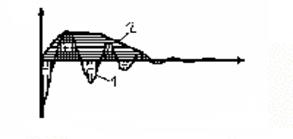
Рисунок 63

В связи с этим для колебательных переходных процессов применяют такие интегральные оценки, знакопеременность подынтегральной функции которых тем или иным способом устранена. Такими оценками являются, например, модульная интегральная оценка (ИМО – интеграл от модуля ошибки):

.

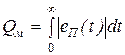И её модификация (ИВМО – интеграл от взвешенного модуля ошибки)

.

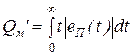Эта оценка придаёт больший вес тем значениям сигнала ошибки, которые имеют место в конце ПП.