Колебательное движение точки

1.Колебаниями можно назвать в механике любые движения тел в ограниченном пространстве. Если через равные промежутки времени движение повторяется во всех деталях, колебания называют периодическими, если нет - апериодическими.

Наиболее важны гармонические колебания, при которых смещение движущейся точки от положения отсчета изменяется по закону синуса или косинуса.

2. Закон гармонического колебательного движенияx = Acos(w t+j₀). (5.1)

Здесь А - амплитуда колебаний, w = 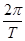- циклическая частота, Т- период колебаний, w t+j₀- фаза колебаний, угловая величина, определяющая положение точки на траектории.

Найдем скорость и ускорение гармонически колеблющейся точки.

v = 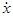= - Aw sin(w t + j₀) = - v_maxsin(w t + j₀). (5.2)

a = 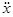= - Aw²cos(w t+j₀) = - a_maxcos(w t+j₀). (5.3)

3. Сложение колебаний, совершающихся вдоль одной прямой, можно сделать методом векторных диаграмм (рис.12).

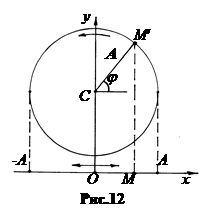Гармоническое колебание точки вдоль оси ОХ интерпретируется как проекция конца вектора, вращающегося в плоскости ХОУ с угловой скоростью w. Вектор А - условный вектор, длина его равна амплитуде колебаний точки.

Различают два случая:

а. частоты колебаний одинаковы,

б. частоты колебаний различны.

а. Cложение колебаний с одинаковыми частотами (рис.13). 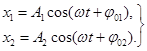(5.4)

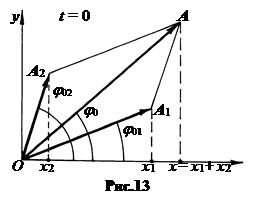Суммарное колебание есть также гармоническое. Действительно, w₁=w₂=w, и весь векторный параллелограмм вращается как одно целое. Амплитуда суммарного колебания A= 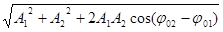, (5.5)

а начальная фаза найдется из формулы:

tgj₀ = 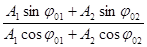. (5.6)

Итак, x=x₁ + x₂ = Acos(w t +j₀). (5.7)