Апериодическая интегральная оценка.

.

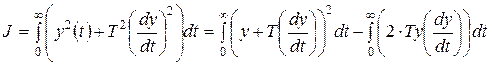Рассмотрим

,

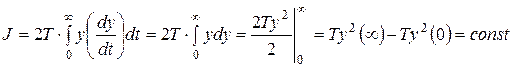т.к. все величины постоянные. Здесь Т – постоянная времени, которая задается.

Если выражение

,

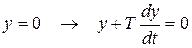то функция J примет минимальное значение. Это будет достигаться в том случае, если у – апериодический переходный процесс.

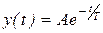- оптимальный процесс с точки зрения апериодической интегральной оценки (рис. 65).

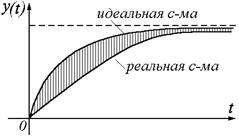
Рисунок 65

Следует отметить, что абсолютное значение любой интегральной оценки само по себе не представляет интереса. Они служат лишь для сопоставления различных вариантов настройки одной и той же системы.

Рекомендованная литература по лекции: [5].

Содержательный раздел 4 «Устойчивость линейных САР»

Лекция 10 «Устойчивые и неустойчивые состояния систем»

10.1 Устойчивость движения.

10.2 Алгебраические критерии устойчивости. Критерий Рауса-Гурвица.

10.3 Положения А.М.Ляпунова.

10.1 Устойчивость движения.

Устойчивость автоматической системы (рис. 66) – это свойство системы возвращаться в исходное состояние равновесия после прекращения воздействия, выведшего систему из этого состояния. Неустойчивая система не возвращается в исходное состояние, а непрерывно удаляется от него.

Рисунок 66 Устойчивость движения:

а) А₀ – невозмущенное состояние, А₂ – возмущенное состояние; на рисунке

б) изображено неустойчивое состояние системы, а на рисунке

в) – ее нейтральное состояние.

По аналогии с состояниями можно ввести понятие возмущенного и невозмущенного движения.

Свободное движение линейной или линеаризованной системы описывается однородным дифференциальным уравнением

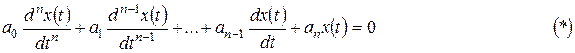
где 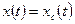- свободная составляющая выходной величины системы.

Система является устойчивой, если свободная составляющая x_c(t) переходного процесса с течением времени стремится к нулю, т.е. если

.

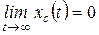Такая устойчивость называется асимптотической.