Апериодическое звено.
Динамика процесса описывается следующим уравнением:
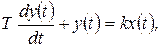
где k - передаточный коэффициент или коэффициент усиления, Т - постоянная времени, характеризующая инерционность звена.
1. Переходная характеристика (рис. 25):
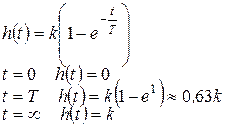
1) 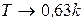
2) В точке ноль строят касательную переходной характеристики, определяют точку пересечения с линией k. Абсцисса этой точки и есть постоянная времени.
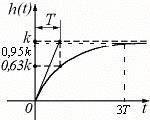
Рисунок 25
2. Импульсная переходная характеристика, или функция веса, звена может быть получена путем дифференцирования функции h(t) (рис. 26):
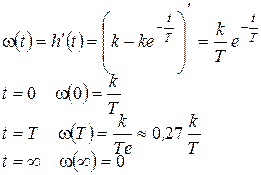
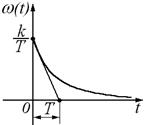
Рисунок 26
3. Передаточная функция:
Применим преобразование Лапласа к уравнению:
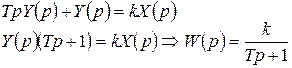 .
.
Структурная схема звена при этом показана на рис. 27.
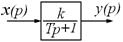
Рисунок 27
4. АФЧХ:
Подставляя в передаточную функцию p=jw, получим амплитудно-фазо-частотную функцию (рис. 28):
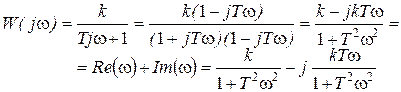
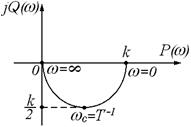
Рисунок 28
 5. АЧХ:
5. АЧХ:
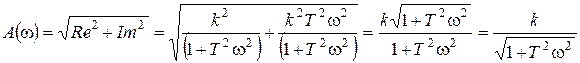
График АЧХ (рис. 29)строится по точкам:
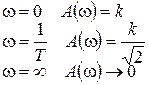
Здесь wс – частота сопряжения.
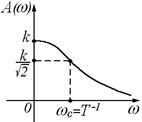
Рисунок 29
Гармонические сигналы малой частоты (w < wс) пропускаются звеном хорошо – с отношением амплитуд выходной и входной величин, близким к передаточному коэффициенту k. Сигналы большой частоты (w > wс) плохо пропускаются звеном: отношение амплитуд существенно < коэффициента k. Чем больше постоянная времени Т, т.е. чем больше инерционность звена, тем меньше АЧХ вытянута вдоль оси частот, или, тем уже полоса пропускания частот.
Таким образом, инерционное звено первого порядка по своим частотным свойствам является фильтром низкой частоты.
6.ФЧХ:
ФЧХ инерционного звена первого порядка (рис. 30) равна:
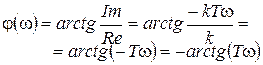
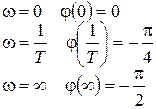
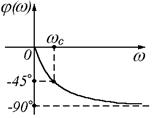
Рисунок 30
Чем больше частота входного сигнала, тем больше отставание по фазе выходной величины от входной. Максимально возможное отставание равно 900. При частоте wс=1/Т сдвиг фаз равен –450.
7.ЛАЧХ:
Рассмотрим теперь ЛАЧХ звена. Точная ЛАЧХ описывается выражением:
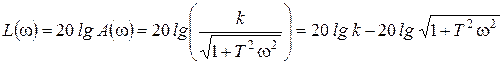 .
.
При построении ЛАЧХ апериодического звена прибегают к асимптотическим методам или, другими словами, строят асимптотический график ЛАЧХ.
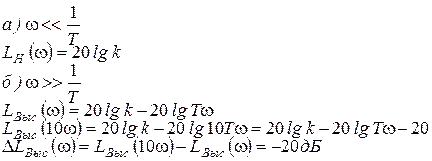
На втором участке наклон асимптотической ЛАЧХ составляет -20 дБ/дек.
Значение сопрягающей частоты wc, при которой пересекаются обе асимптоты, найдем из условия

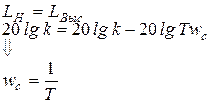
Посмотрим, что будет при построении не асимптотической, а точной ЛАЧХ (рис. 31):
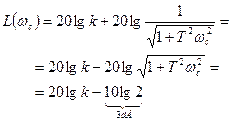
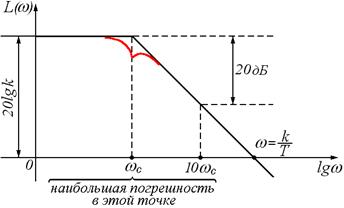
Рисунок 31
Точная характеристика (ЛАЧХ) в точке среза будет меньше асимптотической ЛАЧХ на величину 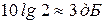 .
.
Дата добавления: 2018-11-26; просмотров: 1257;











