Запаздывающее звено.
Приведём алгебраические дифференциальные уравнения, определяющие перечисленные динамические звенья.
1) Звено называется безынерционным, если между выходной и входной величиной имеется пропорциональная зависимость y = kx. Безынерционные звенья не могут накапливать энергию. Звено считают безынерционным, если его инерционность (постоянная времени), например, на два и более порядков меньше, чем у других звеньев, входящих в автоматическую систему. Примеры: рычаг, шестеренчатая передача, потенциометр, транзисторный усилитель.
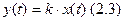
Это линейное алгебраическое уравнение.
k – коэффициент передачи звена на всех частотах.
2) Апериодическое звено 1-ого порядка описывается дифференциальным уравнением первого порядка. Выходная величина в переходных режимах не мгновенно следует за изменениями входной, а постепенно, с конечной скоростью, поэтому это звено инерционное. Примеры: электрическая цепь R-L, электрический двигатель с возбуждением от постоянных магнитов и управляемый током якоря (двигатель, работающий в схеме ведущего стабилизатора ленты).
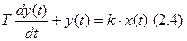
Т – постоянная времени.
k – коэффициент передачи на нулевой частоте.
3) Апериодическое звено 2-ого порядка описывается дифференциальным уравнением второго порядка. Примеры: стабилизатор скорости движения киноленты, электрические преобразователи магнитоэлектрического типа (громкоговорители, зеркальные модуляторы света).
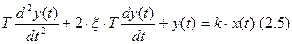
ξ – коэффициент затухания (демпфирования).
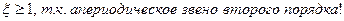
4) Колебательное звено имеет сопряжённые комплексные корни дифференциального уравнения. Временная характеристика колеблется в переходном процессе при приближении к установившемуся значению. Примеры: стабилизатор скорости движения киноленты, электрические преобразователи магнитоэлектрического типа (громкоговорители, зеркальные модуляторы света).
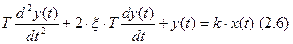
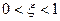
5) Идеальное дифференцирующее звено. Примеры: тахогенератор постоянного тока, работающий в режиме, близком к холостому ходу; операционный усилитель, работающий в режиме дифференцирования.
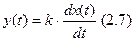
k – это коэффициент передачи для круговой частоты ω = 1 c-1 (потом проверить при выводе).
ω = 2πf (Гц).
6) Идеальное интегрирующее звено. Примеры: малоинерционный и слабо нагруженный электрический двигатель (I≈0), если выходной величиной является угол поворота.
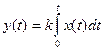
k – это коэффициент передачи для круговой частоты ω = 1 c-1.
7) Запаздывающее звено. Они встречаются в звукотехнических системах, использующих магнитную запись и воспроизведение сигналов звука, системах регулирования температуры обрабатывающих растворов etc.
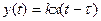
τ – время чистого запаздывания.
В идеальном, типовом запаздывающем звене k = 1.
В технической литературе широко используется символ производной:
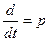
Символ интегрирования:
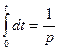
Тогда в символическом виде уравнение из пункта 5 будет выглядеть:
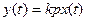
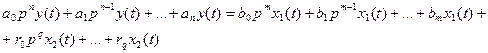
Дата добавления: 2020-10-25; просмотров: 651;











