Основные (типовые) управляющие воздействия САУ
При экспериментальном и теоретическом исследовании автоматических систем и их элементов используют ряд стандартных сигналов, называемых типовыми воздействиями. Эти воздействия описываются простыми математическими функциями и легко воспроизводятся при испытании систем.
Ступенчатое воздействие – это воздействие, которое мгновенно возрастает от нуля до некоторого значения и далее остается постоянным.
Ступенчатому воздействию соответствует функция
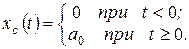
При анализе и расчете систем удобно использовать ступенчатое воздействие, у которого величина а0 = 1. Его называют единичным ступенчатым воздействием и обозначают 1(t).
Ступенчатое воздействие чаще всего используют при испытаниях и расчетах систем стабилизации, так как эти воздействия наиболее близки к реальным входным (задающим и возмущающим) воздействиям систем стабилизации.
Импульсное воздействие представляет собой одиночный импульс прямоугольной формы, имеющий достаточно большую высоту и весьма малую продолжительность (по сравнению с инерционностью испытываемой системы). Очевидно, что площадь такого импульса всегда равна а0.
При математическом анализе автоматических систем используют единичное импульсное воздействие, которое описывается так называемой дельта–функцией

причем
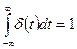 .
.
Согласно этим выражениям, дельта–функцию можно рассматривать как импульс, имеющий бесконечно большую высоту, бесконечно малую длительность и единичную площадь. Дельта–функцию можно определить также как производную единичного скачка:
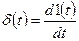 .
.
В качестве стандартного гармонического воздействия используют обычно сигнал синусоидальной формы, описываемый функцией
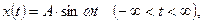
где А – амплитуда сигнала;
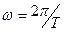 - круговая частота, рад/с;
- круговая частота, рад/с;
Т – период сигнала, с.
Гармонические воздействия широко используются при исследовании точности и устойчивости как стабилизирующих, так следящих и программных автоматических систем. Это объясняется двумя обстоятельствами: во–первых, реальные возмущения часто имеют периодический характер и поэтому могут быть представлены в виде суммы гармонических составляющих; во–вторых, математический аппарат анализа автоматических систем хорошо разработан именно для случая гармонических воздействий.
Для следящих и программных систем типовым является линейное воздействие
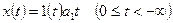 .
.
Коэффициент а1 характеризует скорость нарастания воздействия x(t).
4.2 Передаточные функции.
Передаточной функцией W(p) называют отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях:
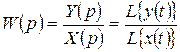 .
.
Передаточная функция также равна отношению входного оператора к собственному оператору:

Как видно, передаточная функция представляет собой некоторый динамический оператор, характеризующий прохождение сигналов через линейный элемент.
Физического смысла у передаточной функции нет.
Часто рассматривают передаточную функцию по управлени
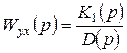
и передаточную функцию по возмущению 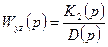 .
.
Рассмотрим основные свойства и особенности передаточных функций.
Передаточная функция элемента связана с его импульсной переходной функцией преобразованием Лапласа:
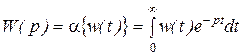 .
.
Учитывая связь между функцией веса и переходной функцией, запишем связь между переходной функцией и передаточной функцией:
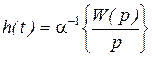 .
.
Для реальных элементов, описываемых обыкновенными дифференциальными уравнениями, передаточная функция представляет собой правильную рациональную дробь
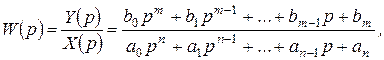
у которой степень многочлена числителя меньше или равна степени многочлена знаменателя, т.е. 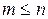 . Все коэффициенты передаточной функции – действительные числа, характеризующие параметры элемента.
. Все коэффициенты передаточной функции – действительные числа, характеризующие параметры элемента.
Для элементов, описываемых передаточной функцией невысокого порядка (n < 3), принято записывать передаточную функцию в стандартной форме. При этом передаточную функцию преобразовывают таким образом, чтобы свободный член знаменателя 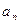 был равен единице. При этом свободный член числителя
был равен единице. При этом свободный член числителя 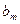 становится равным передаточному коэффициенту и его выносят за скобки:
становится равным передаточному коэффициенту и его выносят за скобки: 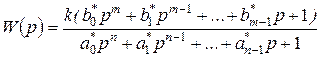 , где
, где 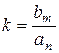 .
.
Передаточная функция является функцией комплексной переменной 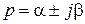 , которая может при некоторых значениях переменной р обращаться в ноль или бесконечность. Значение переменной р, при котором передаточная функция обращается в ноль, называют нулём, а значение, при котором обращается в бесконечность – полюсом передаточной функции. Очевидно, что нулями передаточной функции являются корни полинома
, которая может при некоторых значениях переменной р обращаться в ноль или бесконечность. Значение переменной р, при котором передаточная функция обращается в ноль, называют нулём, а значение, при котором обращается в бесконечность – полюсом передаточной функции. Очевидно, что нулями передаточной функции являются корни полинома 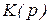 , а полюсами - корни полинома
, а полюсами - корни полинома 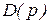 .
.
Рекомендованная литература по лекции: [1].
Лекция 5 «Частотные характеристики САУ»
5.1 Комплексный коэффициент передачи.
5.2 Амплитудно-частотная и фазово-частотная характеристики.
5.1 Комплексный коэффициент передачи.
ККП - комплексный коэффициент передачи.
В системе с нулевыми начальными условиями ККП получается из передаточной функции: 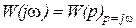 . ККП связывает спектр выходного
. ККП связывает спектр выходного 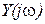 сигнала со спектром входного сигнала
сигнала со спектром входного сигнала 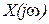 :
: 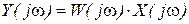 .
.
ККП может быть представлен в виде модуля и аргумента (показательная форма записи комплексной функции): 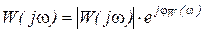 .
.
Спектр синусоидального сигнала  это его комплексная амплитуда
это его комплексная амплитуда 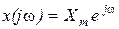 .
.
Тогда 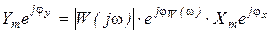 , откуда
, откуда 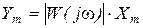 и
и 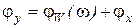 .
.
Таким образом, имеем: 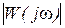 - амплитудно-частотная характеристика (AЧХ),
- амплитудно-частотная характеристика (AЧХ), 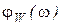 - фазо-частотная характеристика (ФЧХ).
- фазо-частотная характеристика (ФЧХ).
5.2 Амплитудно-частотная и фазово-частотная характеристики.
Зависимость отношения амплитуд выходного и входного сигнала от частоты называют амплитудной частотной характеристикой (сокращенно - АЧХ) и обозначают А(w) (см. рис. 24, а).
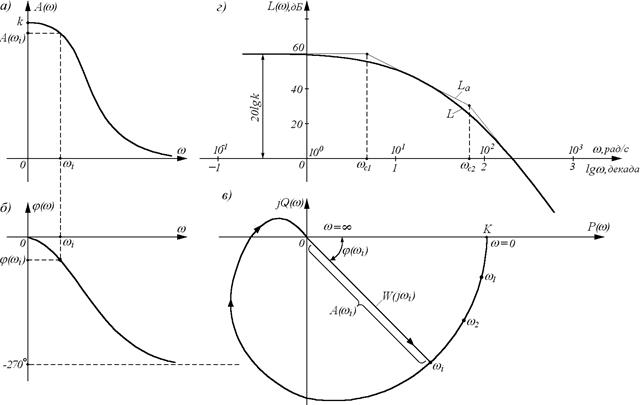
Рисунок 24
Зависимость фазового сдвига между входным и выходным сигналами от частоты называют фазовой частотной характеристикой (ФЧХ) и обозначают j(w) (см. рис. 24, б). Аналитические выражения А(w) и j(w) называют соответственно амплитудной и фазовой частотными функциями.
АЧХ показывает, как элемент пропускает сигналы различной частоты. Оценка пропускания производится по отношению амплитуд 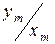 в установившемся режиме. АЧХ имеет размерность, равную отношению размерности выходной величины к размерности входной. ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает элемент при различных частотах в установившемся режиме.
в установившемся режиме. АЧХ имеет размерность, равную отношению размерности выходной величины к размерности входной. ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает элемент при различных частотах в установившемся режиме.
Амплитудную и фазовую частотные характеристики можно объединить в одну общую – амплитудно-фазовую частотную характеристику (АФЧХ или АФХ). Амплитудно-фазовая частотная характеристика W(jw) представляет собой функцию комплексного переменного jw, модуль которой равен А(w), а аргумент равен j(w). Каждому фиксированному значению частоты wi соответствует комплексное число W(jwi), которое на комплексной плоскости можно изобразить вектором, имеющим длину А(wi) и угол поворота j(wi) (см. рис. 24, в). Отрицательные значения j(w), соответствующие отставанию выходного сигнала от входного, принято отсчитывать по часовой стрелке от положительного направления действительной оси.
При изменении частоты от нуля до бесконечности вектор W(jw) поворачивается вокруг начала координат, при этом одновременно увеличивается или уменьшается длина вектора. Кривая, которую при этом опишет конец вектора, называемая годографом, и есть АФЧХ. Каждой точке характеристики соответствует определенное значение частоты.
Проекции вектора W(jw) на действительную и мнимую оси называют соответственно действительной и мнимой частотными характеристиками и обозначают

При этом, действительная частотная характеристика Р(w) – всегда четная функция частоты, а мнимая характеристика Q(w) – всегда нечетная функция.
Аналитическое выражение для АФЧХ конкретного элемента можно получить из его передаточной функции путем подстановки р=jw:
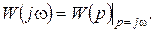
АФЧХ W(jw), как и любая комплексная величина, может быть представлена в показательной форме
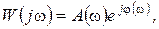
где А(w) – модуль АФЧХ, а j(w) – угол сдвига по фазе;
алгебраической
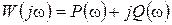 .
.
или тригонометрической
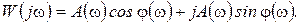
Связь между различными частотными функциями следующая:
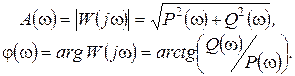
Выделение действительной и мнимой составляющих частотной передаточной функции 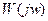 возможно с помощью следующих формул:
возможно с помощью следующих формул:
 ,
,
где 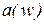 - действительная часть числителя функции
- действительная часть числителя функции 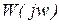
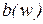 - мнимая часть числителя
- мнимая часть числителя
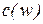 - действительная часть знаменателя
- действительная часть знаменателя
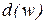 - мнимая часть знаменателя
- мнимая часть знаменателя
При практических расчетах автоматических систем удобно использовать частотные характеристики, построенные в логарифмической системе координат. Такие характеристики называют логарифмическими. Они имеют меньшую кривизну и поэтому могут быть приближенно заменены ломаными линиями, составленными из нескольких прямолинейных отрезков.
За единицу длины по оси частот логарифмических характеристик принимают декаду. Декада – интервал частот, заключенный между произвольным значением wi и его десятикратным значением 10wi. Отрезок логарифмической оси частот, соответствующий одной декаде, равен 1. При построении ЛЧХ по оси абсцисс откладывают логарифм частоты, а подписывают соответствующие значения частот. Ось ординат проводят через произвольную точку.
Обычно в расчетах используют логарифмическую амплитудную частотную характеристику (ЛАЧХ)
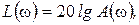
ординаты которой измеряют в логарифмических единицах – белах (Б) или децибелах (дБ).
При построении фазовой частотной характеристики логарифмический масштаб применяют только для оси абсцисс.
На рис.г показаны ЛАЧХ L(w) (толстая линия) и соответствующая ей приближенная (асимптотическая) характеристика Lа(w) в виде прямолинейных отрезков (тонкая линия). Частоты, соответствующие точкам стыковки отрезков, называют сопрягающими и обозначают wс.
По виду частотных характеристик все элементы и системы делят на 2 группы: минимально-фазовые и неминимально-фазовые. Минимально-фазовые – такие, у которых все нули и полюса передаточной функции имеют отрицательные действительные части. Такие элементы дают минимальный фазовый сдвиг по сравнению с любыми другими элементами, имеющими такую же амплитудную характеристику, но у которой действительная часть хотя бы одного полюса или нуля положительна. Для примера, звенья 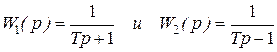 имеют одинаковые ЛАЧХ, но разные ЛФЧХ.
имеют одинаковые ЛАЧХ, но разные ЛФЧХ.
Рекомендованная литература по лекции: [5].
Содержательный раздел 3 «Линейные САУ»
Лекция 6 «Типовые динамические звенья линейных систем»
6.1 Классификация. Простейшие звенья. Звенья первого, второго и третьего порядка.
6.2 Апериодические и колебательные звенья.
6.3 Звено запаздывания.
6.1 Классификация. Простейшие звенья. Звенья первого, второго и третьего порядка.
Алгоритмические звенья, которые описываются обыкновенными дифференциальными уравнениями первого и второго порядка, получили название типовых динамических звеньев.
Типовые динамические звенья являются основными составными частями алгоритмических структур непрерывных систем управления,  знание их характеристик существенно облегчает анализ таких систем.
знание их характеристик существенно облегчает анализ таких систем.
Классификацию (табл. 2) удобно осуществить, рассматривая различные частные формы дифференциального уравнения:
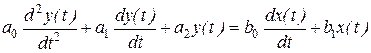 .
.
Звенья, у которых а2 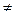 0 и в1
0 и в1 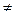 0 обладают статизмом , т.е. однозначной связью между входной и выходной переменными в статическом режиме. Звенья – статические, или позиционные.
0 обладают статизмом , т.е. однозначной связью между входной и выходной переменными в статическом режиме. Звенья – статические, или позиционные.
Звенья, у которых 2 из трех коэффициентов а2 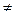 0, а1
0, а1 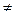 0, а0
0, а0 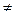 0, обладают инерционностью (замедлением).
0, обладают инерционностью (замедлением).
Таблица 2 – Классификация звеньев. Типовые динамические звенья
| № | Наименование | а0 | а1 | а2 | в0 | в1 | Примечания | W(p) |
| Безынерционное (пропорциональное) | к | Статическое элементарное | ||||||
| Инерционное первого порядка (апериодическое) | Т | к | Статическое инерционное | |||||
| Инерционное второго порядка (апериодическое) | Т22 | Т1 | к | Т1 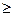 2Т2 Статическое
инерционное 2Т2 Статическое
инерционное
| ||||
| Инерционное второго порядка (колебательное) | Т22 | Т1 | к | Т1 <2Т2 Статическое инерционное | ||||
| Идеальное интегрирующее | к | элементарное | ||||||
| Реальное интегрирующее | Т | к | инерционное | |||||
| Идеальное дифференцирующее | к | элементарное | ||||||
| Реальное дифференцирующее | Т | к | инерционное | |||||
| Изодромное (пропорционально- интегрирующее) | к1 | к | ||||||
| Форсирующее (пропорционально- дифференцирующее) | к1 | к | Статическое | |||||
| Упругое (интегро- дифференцирующее, реально-форсирующее) | Т | к1 | к | 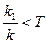 -преобладают
интегрирующие свойства -преобладают
интегрирующие свойства
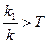 -преобладают
дифференцирующие
свойства
Статическое, инерционное -преобладают
дифференцирующие
свойства
Статическое, инерционное
|
У звеньев 1,5,7 только 2 коэффициента 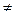 0. Они являются простейшими, или элементарными. Все остальные типовые звенья могут быть образованы из элементарных путем последовательного, параллельного и встречно-параллельного соединения.
0. Они являются простейшими, или элементарными. Все остальные типовые звенья могут быть образованы из элементарных путем последовательного, параллельного и встречно-параллельного соединения.
6.2 Апериодические и колебательные звенья.
Дата добавления: 2018-11-26; просмотров: 1683;











