Другим видом маятника является любое физическое тело, подвешенное за какую либо точку тела и имеющее возможность совершать колебательное движение.

Физический маятник

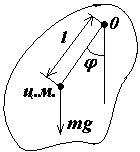Возьмем произвольное тело, пронзим его в какой либо точке несовпадающей с его центром масс осью вокруг которой тело может свободно поворачиваться. Подвесим тело на этой оси, и отклоним его из положения равновесия на некоторый угол j .

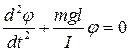Тогда на тело с моментом инерции I относительно оси О будет действовать возвращающий в положение равновесия момент М = -mglsinj и колебания физического маятника как и математического будут описываться дифференциальным уравнением:

Так как для разных физических маятников момент инерции будет выражаться по разному, то его не будем расписывать как в случае с математическим маятником. Это уравнение так же имеет вид уравнения колебаний, решением которого являются функции описывающие гармонических колебаний. При этом циклическая частота (w), период колебаний (Т) определяются как:

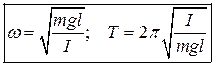
Мы видим, что в случае физического маятника период колебаний зависит от геометрии тела маятника, а не от его массы , как и в случае математического маятника. Действительно в выражение для момента инерции входит масса маятника в первой степени. Момент инерции в выражении для периода колебаний стоит в числителе, в то время как масса маятника входит в знаменатель и тоже в первой степени. Таким образом, масса в числителе сокращается с массой в знаменателе.

Физический маятник обладает еще одной характеристикой это приведенная длина.