С) Теорема линейности.
Линейность D – преобразования.
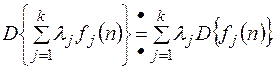
С) Смещение в области оригиналов.
Если 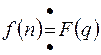 , то
, то
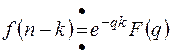
и 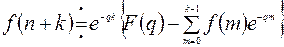 .
.
С) Теорема затухания.
Смещение в области изображений.
Если 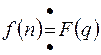 , то
, то
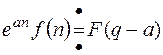 .
.
Эти свойства доказываются непосредственным применением формулы D – преобразования.
С) Теорема о разности решетчатой функции.
Изображение конечных разностей.
Если 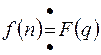 , то
, то
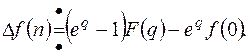
Доказательство:
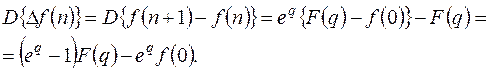
ч.т.д.
Если функция 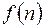 допускает D – преобразование, то её разность произвольного порядка к также допускает D – преобразование, поскольку разность
допускает D – преобразование, то её разность произвольного порядка к также допускает D – преобразование, поскольку разность 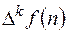 представима в виде линейной комбинированной решетчатой функции
представима в виде линейной комбинированной решетчатой функции 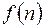 ,
, 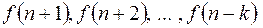 .
.
Многократно применяя предыдущую формулу нетрудно получить
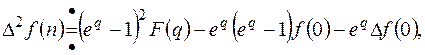
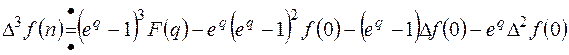 ,…
,…
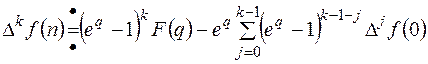 .
.
Последняя формула значительно упрощается, если решетчатая функция обращается в ноль при n=0,1,…, к-1:
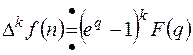 .
.
С) Теорема о сумме решетчатой функции.
Изображение конечной суммы.
Если 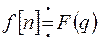 , то
, то
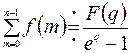 .
.
Пусть 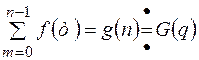 , т.к.
, т.к. 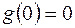 , то применяя теорему о разности
, то применяя теорему о разности 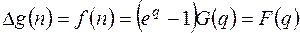 т.о.
т.о.
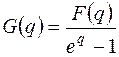 .
.
С) Дифференцирование изображений.
Если 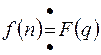 , то
, то
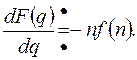
Доказать можно дифференцированием ряда выражающего D – преобразование.
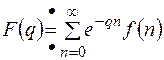 ,
,
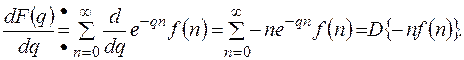
Дата добавления: 2021-11-16; просмотров: 445;











