Вторая теорема подобия. Уравнения подобия
Решение системы уравнений, описывающих какое-либо явление, может быть представлено в виде зависимости между критериями подобия, получаемыми из этой системы уравнений.
Например, уравнение теплоотдачи можно представить в следующем безразмерном виде 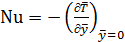 .
.
В таком виде оно является безразмерным уравнением теплоотдачи относительно критерия 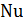 , который является функцией искомой величины
, который является функцией искомой величины 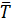 .
.
Если к этому уравнению добавить безразмерное уравнение переноса теплоты 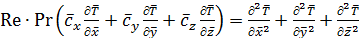 , то получим систему уравнений для определения
, то получим систему уравнений для определения 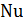 , т.к. критерии
, т.к. критерии 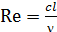 и
и 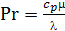 определяются через известные величины, поэтому известны.
определяются через известные величины, поэтому известны.
Таким образом, эту систему уравнений можно рассматривать как систему относительно новых безразмерных переменных, которые разделяются на две группы:
- независимые или определяющие, которые составлены только из размерных величин, т.е. 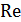 ,
, 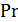 ,
, 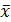 ,
,  ;
;
- зависимые или определяемые, составленные из искомых размерных величин, т.е. 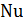 ,
, 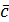 и
и 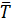 .
.
Согласно второй теореме подобия, решение приведенной выше системы дифференциальных уравнений может быть представлено в виде следующего критериального уравнения: 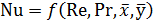 .
.
Таким образом, результаты исследований можно представить в виде критериальных уравнений, а не только в виде функциональной связи между размерными величинами.
Преимуществом такого способа является то, что число критериев подобия
меньше числа размерных величин, входящих в исходную систему размерных уравнений.
Например, для определения коэффициента теплоотдачи в размерной системе уравнений необходимо установить его зависимость от следующих величин: 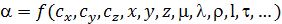 .
.
А для определения 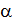 (т.е.
(т.е. 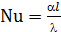 ) из уравнения
) из уравнения 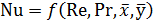 необходимо определить зависимость
необходимо определить зависимость 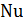 лишь от четырех величин, что значительно упрощает задачу.
лишь от четырех величин, что значительно упрощает задачу.
Дата добавления: 2021-06-28; просмотров: 777;











