Главный вектор и главный момент. Теорема Пуансо
Теорема Пуансо. Любая произвольная система сил, приложенных к твердому телу, эквивалентна системе, состоящей из одной силы, приложенной в какой-либо точке О тела и одной пары.
Такой процесс замены системы сил одной силой и парой сил называют приведением системы сил к заданному центру.
Пусть дана произвольная система сил 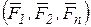 (рис.5.7а), приложенных к твердому телу. Выберем произвольную точку О тела за центр приведения и каждую силу заданной системы сил приведем к точке О (рис.5.7б).
(рис.5.7а), приложенных к твердому телу. Выберем произвольную точку О тела за центр приведения и каждую силу заданной системы сил приведем к точке О (рис.5.7б).
Таким образом, система из n сил заменена системой сходящихся сил, приложенных в точке О, и системой присоединенных пар сил. Векторные моменты присоединенных пар сил можно заменить одной парой согласно формуле (3.1), момент которой
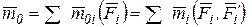 .
.
Систему сходящихся сил (F1,F2, Fn) заменим вектором 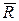 , который равен векторной сумме сил:
, который равен векторной сумме сил:
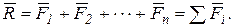 (5.6)
(5.6)
| а | 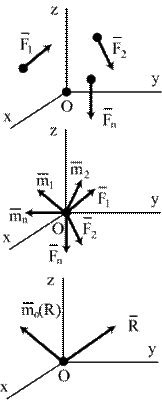
| Принято называть вектор 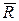 главным вектором системы сил, а вектор главным вектором системы сил, а вектор 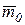 главным моментом относительно центра О (рис.5.7в).
Главным вектором системы сил называют вектор, равный векторной сумме этих сил.
Главным моментом системы сил относительно центра О называют сумму векторных моментов всех сил системы относительно этого центра.
Таким образом, основную теорему статики (теорему Пуансо) в краткой форме можно выразить так: произвольную главным моментом относительно центра О (рис.5.7в).
Главным вектором системы сил называют вектор, равный векторной сумме этих сил.
Главным моментом системы сил относительно центра О называют сумму векторных моментов всех сил системы относительно этого центра.
Таким образом, основную теорему статики (теорему Пуансо) в краткой форме можно выразить так: произвольную
|
| б | ||
| в | ||
| Рис.5.7 |
систему сил можно привести к главному вектору  , приложенному в центр приведения, и главному моменту
, приложенному в центр приведения, и главному моменту 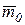 относительно этого центра приведения.
относительно этого центра приведения.
Приведем формулы для вычисления главного вектора и главного момента.
Для любой произвольной системы сил
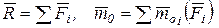 . (5.9)
. (5.9)
Проецируя 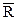 на оси координат, получаем:
на оси координат, получаем:
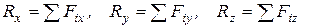 . (5.10)
. (5.10)
По проекциям определяют модуль главного вектора, а направление - по направляющим косинусам:
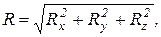 (5.11)
(5.11)
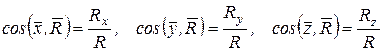 .
.
Главный момент 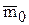 тоже имеет проекции на оси координат mx, my, mz, которые можно определить, используя связь момента силы относительно оси с проекцией векторного момента этой силы относительно точки на оси. Тогда
тоже имеет проекции на оси координат mx, my, mz, которые можно определить, используя связь момента силы относительно оси с проекцией векторного момента этой силы относительно точки на оси. Тогда
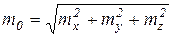 , (5.12)
, (5.12)
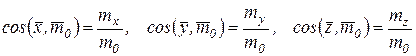 .
.
Дата добавления: 2019-12-09; просмотров: 1417;











