C) Теорема затухания (Теорема смещения)
Для любого 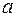 имеет место соотношение
имеет место соотношение
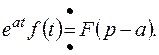
Умножение оригинала на функцию 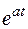 влечет смещение переменной р на
влечет смещение переменной р на 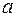 .
.
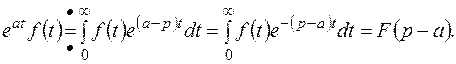
Следствие:
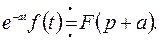
4с) Теорема запаздывания.
Для любого постоянного 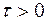 :
:
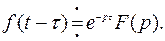
.
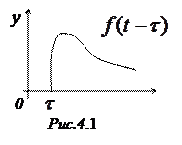 |

Т.о. запаздывание оригинала на время 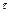 соответствует умножение изображения на
соответствует умножение изображения на 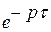 (рис.4.1).
(рис.4.1).
Доказательство:
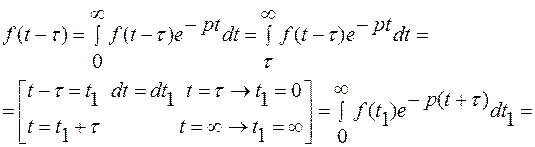
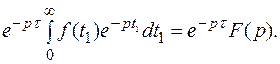
Теорема запаздывания играет важную роль в связи с тем, что с ее помощью можно получать изображения функций часто встречающихся в технических приложениях - функций, которые имеют различные аналитические выражения в различных промежутках значений аргумента.
Пример. Найти изображение единичного импульса:
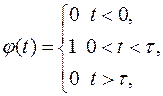 (рис.4.2).
(рис.4.2).
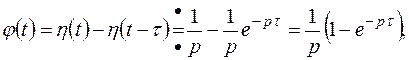
Итак, 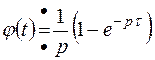
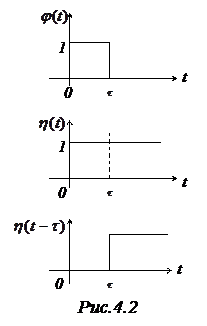 |
 Пример. Найти изображение единичного импульса длительного
Пример. Найти изображение единичного импульса длительного 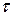 , начинающегося в момент времени
, начинающегося в момент времени 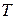 (рис.4.3).
(рис.4.3).
Эту функцию можно представить как предыдущую, сдвинутую на 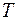 , т.е. нужно найти изображение функции
, т.е. нужно найти изображение функции 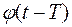 , если изображение функции
, если изображение функции 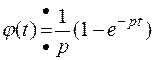 ,
,
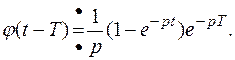
Пример. Найти изображение последовательности импульсов (рис.4.4).
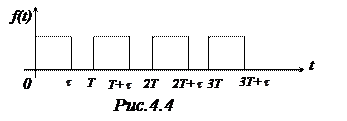 |
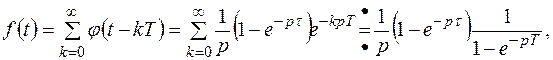
итак 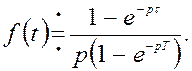

C) Теорема опережения.
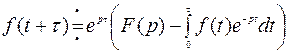 (рис.4.5).
(рис.4.5).
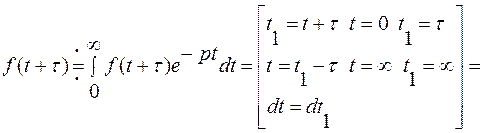
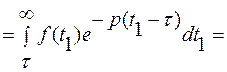
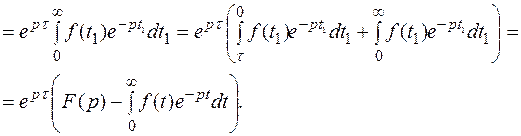
Дата добавления: 2021-11-16; просмотров: 1073;











