Определение дискретного преобразования Лапласа.

Дискретное преобразование Лапласа определяется формулой

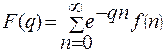(11.12)

где 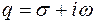- комплексная переменная,

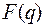называется изображением,

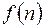- решетчатая функция.

Дискретное преобразование Лапласа также называют D - преобразованием и обозначают 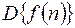, т.е.

.

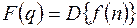Наряду с D – преобразованием применяется так называемое Z – преобразование.

Z – преобразование определяется формулой (1) в которую вводится новая переменная

.

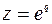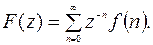(11.13)

Z – преобразование обозначают так:

.

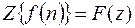Если известно изображение 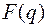некоторой решетчатой функции, то соответствующее изображение 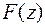может быть найдено с помощью замены комплексной переменной q по формуле

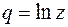, тогда

.

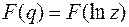Аналогично можно определить изображение 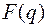по заданной функции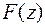

.

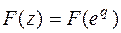Т.о. принципиальной разницы между D – преобразованием и Z – преобразованием не существует. Все основные свойства Z – преобразования могут быть получены из соответствующих свойств D – преобразования.

В выражении (11.12) справа стоит ряд, который сходится абсолютно в каждой точке полуплоскости 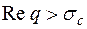, сходится равномерно в каждой полуплоскости 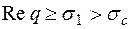и

расходится в полуплоскости 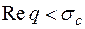(рис.11.2).

Величина 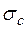называется абсциссой абсолютной сходимости D – преобразования (11.12).

Т.о. область сходимости D – преобразования есть полуплоскость, расположенная справа от прямой 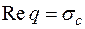(рис.11.2).

Если в частности 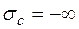, то ряд (11.12) сходится всюду, если же 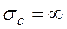, то D – преобразования не существует.

Так же можно сказать, что функция 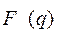является аналитической в полуплоскости .

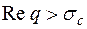По аналогии с непрерывным преобразованием Лапласа, будем называть оригиналом решетчатую функцию 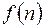, которая равна нулю при n<0 и удовлетворяет при 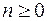условию

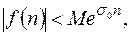
где М>0 и 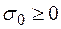некоторые постоянные величины. Величина 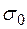называется показателем роста решетчатой функции .

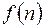Теорема. Для всякого оригинала 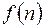изображение 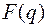определено в полуплоскости 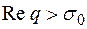и является в этой полуплоскости аналитической функцией.

Непосредственно из определения D – преобразования по формуле (1) следует, что функция 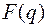является периодической вдоль мнимой оси плоскости q с периодом .

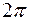Действительно,

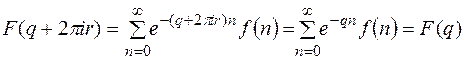
где r – любое целое число.

Поэтому достаточно изучить свойства функции 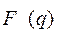в любой полосе шириной 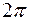. Наиболее удобна для этой цели полоса

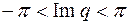. (рис.11.3).

Эту полосу удобно называть основной полосой.

Формула обращения.

Преобразование обратное по отношению к дискретному преобразованию Лапласа определяет решетчатую функцию 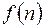по заданному изображению 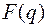и определяется формулой

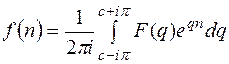(11.14)

где С > .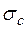

Вычисление оригиналов 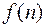можно производить и по формуле обращения Z – преобразования, которая может быть получена из формулы (11.14) путем замены переменной .

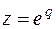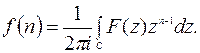(11.15)

Интегрирование производится по окружности С радиуса 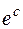, где С> 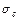в положительном направлении. Функция, стоящая под интегралом 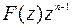- аналитическая вне окружности С и на самой окружности. Применяя теорему о вычетах получим:

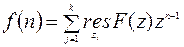, (11.16)

где 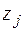- полюс функции 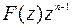, лежащий внутри окружности С.

Иногда оказывается более удобным определять вычеты, не переходя к Z – преобразованию. Тогда формула (11.16) принимает вид

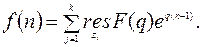(11.17)

Пример.

Найти оригинал 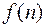, соответствующий изображению

.

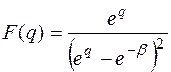Решение. Выполним замену переменной

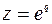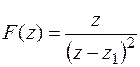, , где .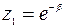

Образуем функцию

.

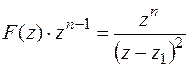Находим вычет в точке 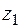- это двукратный полюс

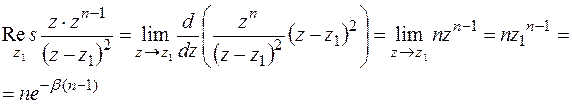
Таким образом,

.

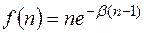Свойства дискретного преобразования Лапласа.

Дискретное преобразование Лапласа устанавливает соответствие между решетчатыми функциями – оригиналами 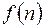и их изображениями 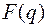. Различным операциям, совершаемыми над решетчатыми функциями, соответствуют при этом определенные операции, совершаемые над их изображениями.