Конечные разности решетчатых функций.
Выражение
 (11.1)
(11.1)
называется конечной разностью первого порядка решетчатой функции, или просто первой разностью.
Ясно, что 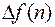 - представляет собой решетчатую функцию, для которой может быть вычислена конечная разность. Т.о. первая разность от решетчатой функции
- представляет собой решетчатую функцию, для которой может быть вычислена конечная разность. Т.о. первая разность от решетчатой функции 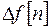 называется разностью второго порядка решетчатой функции
называется разностью второго порядка решетчатой функции 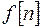 , или просто второй разностью
, или просто второй разностью
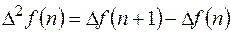 (11.2)
(11.2)
Разность к – го порядка решетчатой функции 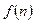 определяется формулой
определяется формулой
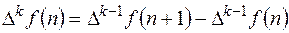 (11.3)
(11.3)
Разность любого порядка можно выразить через значения решетчатой функции 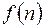 .
.
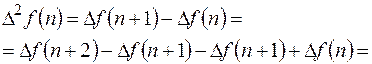
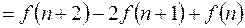 (11.4)
(11.4)
Аналогично для третьей разности:
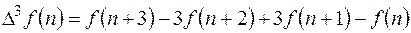 (11.5)
(11.5)
Для разности произвольного порядка к справедлива формула
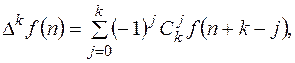 (11.6)
(11.6)
где 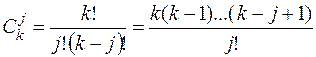 . так называемые биноминальные коэффициенты, такие что:
. так называемые биноминальные коэффициенты, такие что:
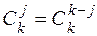 .
.
Пример.
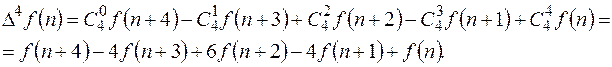
Формулы (11.1)-(11.6) позволяют выразить саму решетчатую функцию 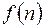 через её разности различных порядков.
через её разности различных порядков.
Из (11.1)
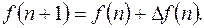 (11.7)
(11.7)
Из (11.2)
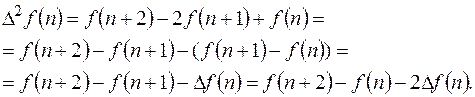
откуда
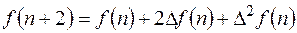 . (11.8)
. (11.8)
Используя равенство (11.3) при к=3 и равенства (11.4), (11.7), (11.8) получим
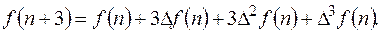 (11.9)
(11.9)
Продолжая вычисления можно получить общую формулу
 , (11.10)
, (11.10)
при n=0
 (11.11)
(11.11)
Формулы (11.10) и (11.11) выражают значения решетчатой функции через её конечные разности до порядка l включительно. Эти формулы являются дискретным аналогом разложения непрерывных функций в ряд Тейлора.
Примеры.
1). 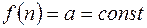 ,
,
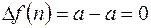 .
.
2). 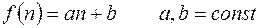 .
.
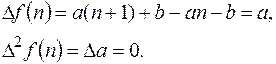
3). 
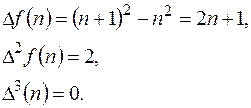
4). 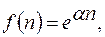
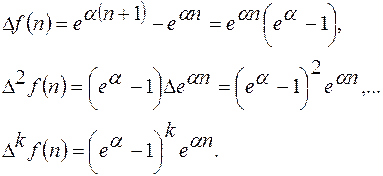
Отметим, что операция взятия конечных разностей является линейной операцией, что следует из определения конечной разности
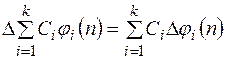 .
.
Используя выражение (11.1), можно вывести формулу для вычисления разности произведений 2-х функций
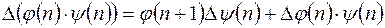 .
.
Дата добавления: 2021-11-16; просмотров: 445;











