РЕШЕНИЕ РАЗНОСТНЫХ УРАВНЕНИЙ
Всякое соотношение, связывающее решетчатую функцию 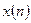 и её разности до некоторого порядка к
и её разности до некоторого порядка к
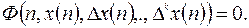 (12.1)
(12.1)
называется разностным уравнением.
Используя формулу, выражающую разности различных порядков через значения решетчатой функции
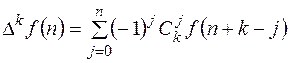
можно соотношение (12.1)преобразовать к виду
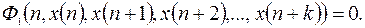 (12.2)
(12.2)
Если (12.2) содержит в явном виде функции 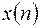 и
и 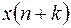 , то исходное разностное уравнение (12.1) называют уравнением порядка к.
, то исходное разностное уравнение (12.1) называют уравнением порядка к.
При переходе от разностей решетчатых функций к самим решетчатым функциям могут взаимно уничтожаться как функции 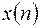 , так и функции
, так и функции 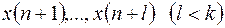 . И в результате порядок разностного уравнения может отличаться от порядка старшей разности.
. И в результате порядок разностного уравнения может отличаться от порядка старшей разности.
Например.
Дано уравнение
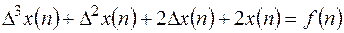 .
.
Используя выражение для разностей, имеем
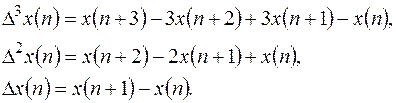
Подставляем в уравнение, после приведения подобных членов получим.
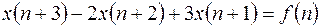 .
.
Введем новую переменную m=n+1. Получим
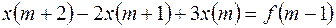 .
.
Т.о. исходное уравнение является уравнением второго порядка, несмотря на то, что оно содержит разность третьего порядка.
Решетчатая функция 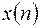 , которая обращает уравнение в тождество, называется решением разностного уравнения.
, которая обращает уравнение в тождество, называется решением разностного уравнения.
Мы ограничимся рассмотрением лишь линейных разностных уравнений к – го порядка с постоянными коэффициентами
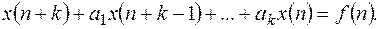 (12.3)
(12.3)
Если 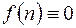 , то уравнение называется однородным.
, то уравнение называется однородным.
Пусть заданы значения 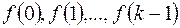 - начальные значения. Применяя к обеим частям уравнения (12.3) дискретное преобразование Лапласа и пользуясь свойством 2 – смещение в области оригиналов (теорема опережения), получим уравнение относительно
- начальные значения. Применяя к обеим частям уравнения (12.3) дискретное преобразование Лапласа и пользуясь свойством 2 – смещение в области оригиналов (теорема опережения), получим уравнение относительно 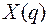 - изображения искомой функции
- изображения искомой функции 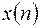 . Решаем это алгебраическое уравнение относительно
. Решаем это алгебраическое уравнение относительно 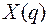 . Далее, пользуясь таблицами или формулами обратного преобразования, получим
. Далее, пользуясь таблицами или формулами обратного преобразования, получим 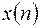 .
.
Если начальные значения не заданы, то, считая их произвольными постоянными получим общее решение уравнения (12.3).
Если исходное линейное разностное уравнение записано в виде
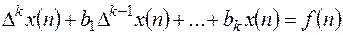 (12.4)
(12.4)
то метод его решения остается тем же. Но для перехода от оригинала к изображению в левой части уравнения следует воспользоваться свойством 4 – изображением конечных разностей. При этом должны быть заданы начальные значения
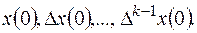
Если эти значения не заданы, то, считая их произвольными постоянными, получим общее решение.
Указанный метод применяется и при решении систем разностных уравнений.
Пример 1.
Найти решение уравнения
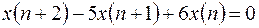
при начальных условиях
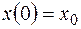
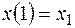 .
.
Решение:
Пусть 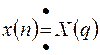
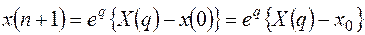
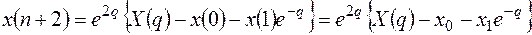
Подставляем в уравнение
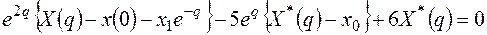 .
.
Откуда находим 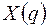 .
.
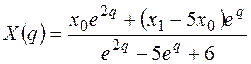 .
.
Удобно произвести замену 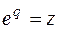 .
.
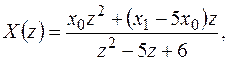 тогда оригинал:
тогда оригинал:
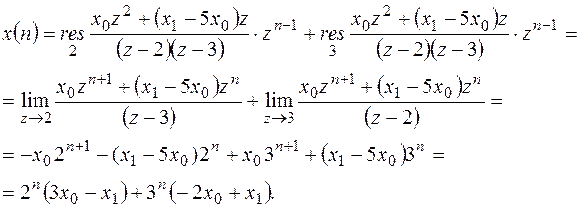
В таблице 3 приведены наиболее часто встречающиеся в примерах соответствия при D-преобразовании и Z - преобразовании.
Пример 2.
Найти решение уравнения 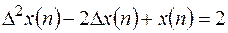 при начальных условиях
при начальных условиях 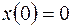 ,
, 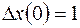 .
.
Решение. Здесь уравнение дано в форме разности. Применяем Z – преобразование к обеим частям уравнения:
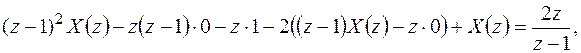
Откуда,
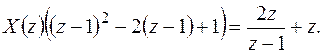
Таблица 3
| № | 
| 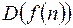
| 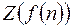
|
| 1. | 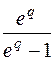
| 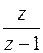
| |
| 2. | 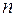
| 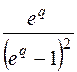
| 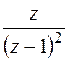
|
| 3. | 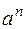
| 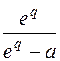
| 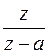
|
| 4. | 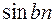
| 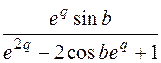
| 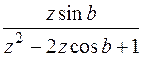
|
| 5. | 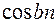
| 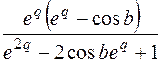
| 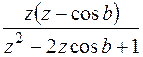
|
| 6. | Линейность
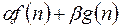
| 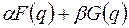
|  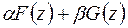
|
| 7. | Опережение
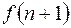
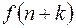
| 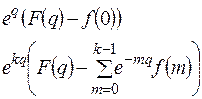
| 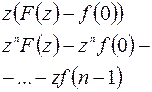
|
| 8. | Запаздывание
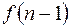
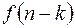
|
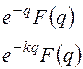
|
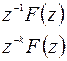
|
| 9. | Дифференцирование
изображения
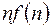
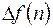
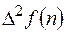
|
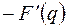
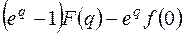
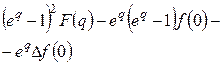
|
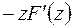
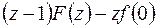
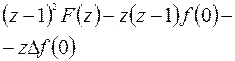
|
Решая это уравнение относительно 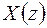 , получим:
, получим:
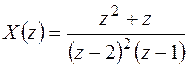 .
.
Возвращаемся к оригиналу:
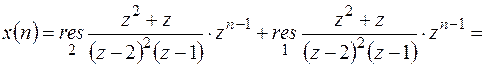
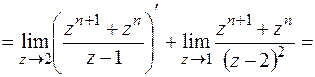
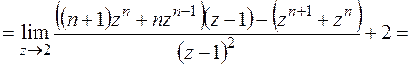
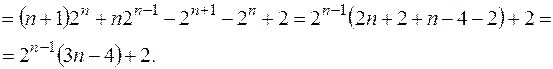
Пример 3. Найти решение уравнения x(n+2)+4x(n+1)+3x(n)=1, при начальных условиях x(0)=1, x(1)=1.
Решение.
Применяем Z – преобразование к обеим частям уравнения:
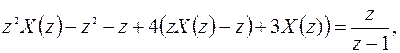 откуда получаем:
откуда получаем:
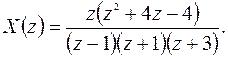
Возвращаясь к оригиналу, получим:
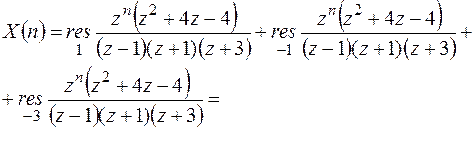
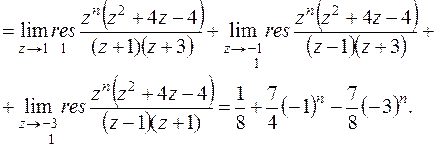
Дата добавления: 2021-11-16; просмотров: 455;











