С) Интегрирование изображений.

Если 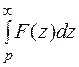сходится, то

.

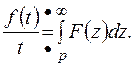Интегрирование изображения в пределах от р до 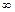соответствует делению оригинала на t.

Доказательство:

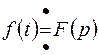
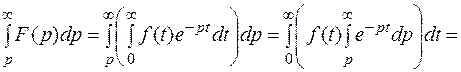
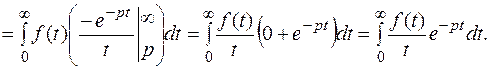
Этот интеграл – есть изображение по Лапласу функции .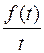

Пример. Найти изображение функции .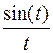

Решение:

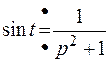, тогда

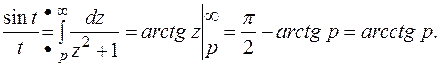
С) Теорема умножения изображений (теорема Бореля)

Рассмотрим некоторые понятия:

сверткой двух функций f(t) и g(t) называется интеграл

.

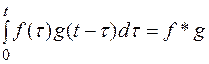Этот интеграл является функцией переменной t.

Свертка коммутативна f*g=g*f.

Если f и g – оригиналы, то и f*g тоже оригинал.

Операции свертки оригиналов соответствует произведение изображений.

.

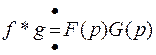Это и есть теорема умножения изображений Бореля.

Доказательство:

.

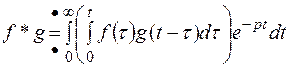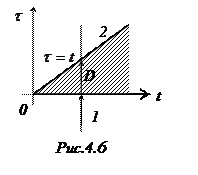Рассмотрим это выражение как двойной интеграл по бесконечной области D (рис.4.6).

Пределы интегрирования:

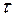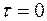по от до ;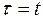

по t от 0 до .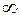

Изменим порядок интегрирования

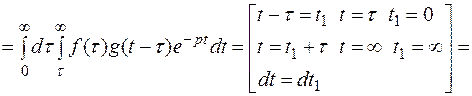
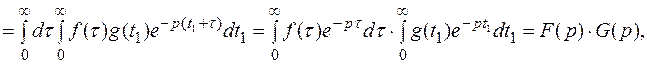ч.т.д.

Рассмотрим специальный случай теоремы умножения. Найдем оригинал изображения pF(p)G(p)

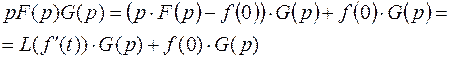, тогда по теореме Бореля

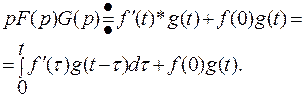
Эта формула носит название интеграл Дюамеля.