ИЗОБРАЖЕНИЕ ПО ЛАПЛАСУ
Изображением по Лапласу функции-оригинала 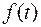 называется комплекснозначная функция
называется комплекснозначная функция 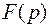 комплексного аргумента
комплексного аргумента 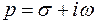 , определяемая соотношением
, определяемая соотношением 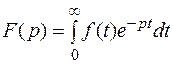 .
.
Соответствие между оригиналом 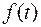 и изображением
и изображением 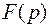 символически записывается так:
символически записывается так:
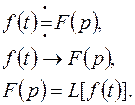
Или обратное:
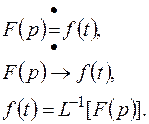
Здесь L - оператор прямого преобразования Лапласа,
L-1- оператор обратного преобразования Лапласа.
Итак, преобразование Лапласа является оператором, который каждой функции 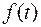 ставит в соответствие функцию
ставит в соответствие функцию 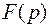 .
.
Заметим, что метод Хевисайда, как это стало ясно после работ Карсона, заключается в переходе от функции 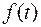 к функции
к функции 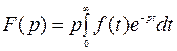 .
.
Таким образом, изображение по Хевисайду отличается от изображения по Лапласу множителем 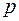 .
.
Наличие дополнительного множителя 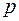 приближает метод Хевисайда к другому символическому методу, применяемому в электротехнике (методу Карсона), однако, оно вносит неоправданные усложнения в некоторые выкладки. Кроме того, преобразование Лапласа более естественно связывается с известным преобразованием Фурье, которое широко применяется в математической физике. Исходя из этих соображений, будем рассматривать преобразование Лапласа, а не преобразование Хевисайда.
приближает метод Хевисайда к другому символическому методу, применяемому в электротехнике (методу Карсона), однако, оно вносит неоправданные усложнения в некоторые выкладки. Кроме того, преобразование Лапласа более естественно связывается с известным преобразованием Фурье, которое широко применяется в математической физике. Исходя из этих соображений, будем рассматривать преобразование Лапласа, а не преобразование Хевисайда.
Имеет место следующая теорема о существовании изображения по Лапласу.
Теорема:
Пусть функция 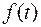 является оригиналом, тогда интеграл Лапласа сходится абсолютно для всех значений комплексной переменной
является оригиналом, тогда интеграл Лапласа сходится абсолютно для всех значений комплексной переменной 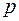 , удовлетворяющих условию:
, удовлетворяющих условию: 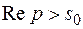 и определяет изображение
и определяет изображение 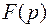 , которое является аналитической функцией в полуплоскости
, которое является аналитической функцией в полуплоскости 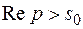 .
.
Для доказательства оценим модуль интеграла Лапласа:
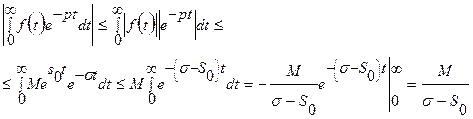 , если
, если 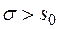 .
.
Итак: 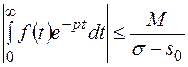 , что и говорит о абсолютной сходимости интеграла Лапласа.
, что и говорит о абсолютной сходимости интеграла Лапласа.
Чтобы доказать аналитичность 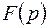 найдем производную:
найдем производную:

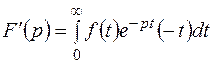 .
.
Аналогично предыдущему можно показать: полученный интеграл сходится, значит, 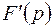 существует, и функция
существует, и функция 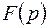 аналитична в полуплоскости
аналитична в полуплоскости 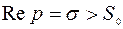 (рис.2.1).
(рис.2.1).
Следствие:
Так как 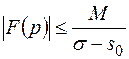 , то
, то 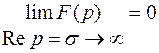 , а если
, а если 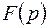 аналитична в бесконечно удаленной точке, то
аналитична в бесконечно удаленной точке, то 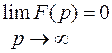 , т.е. имеет нуль в бесконечно удаленной точке.
, т.е. имеет нуль в бесконечно удаленной точке.
Замечания.
1. 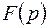 обычно имеет изолированные особые точки
обычно имеет изолированные особые точки 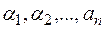 и поэтому определена не только в полуплоскости
и поэтому определена не только в полуплоскости 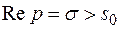 , а всюду при
, а всюду при 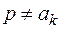 ,
, 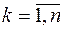 (Рис.3). Однако
(Рис.3). Однако 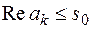 при
при 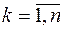 .
.
2. Преобразование Лапласа относится к семейству интегральных преобразований типа:
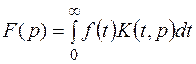 , где
, где 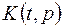 - ядро преобразования.
- ядро преобразования.
Если
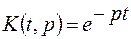 имеем преобразование Лапласа,
имеем преобразование Лапласа,
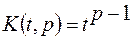 преобразование Меллина,
преобразование Меллина,
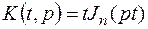 преобразование Ханкеля,
преобразование Ханкеля,
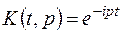 преобразование Фурье
преобразование Фурье 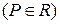 ,
,
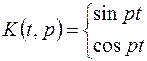 ,- синус и косинус преобразования Фурье
,- синус и косинус преобразования Фурье 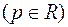 .
.
Дата добавления: 2021-11-16; просмотров: 526;











