ФОРМУЛА ОБРАЩЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА

Из математического анализа известно экспоненциальное преобразование Фурье абсолютно интегрируемой функции :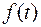

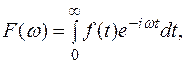
и формула его обращения:

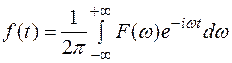- интеграл понимается в смысле главного значения.

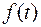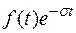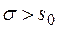Пусть - функция-оригинал. Тогда при будет абсолютно интегрируемой и ее можно преобразовать по Фурье:

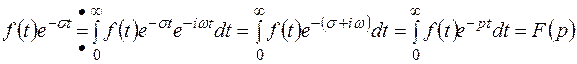- преобразование по Лапласу для функции

Таким образом, получили: преобразование по Фурье 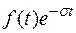есть преобразование по Лапласу функции .

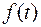Тогда из формулы обращения преобразования Фурье получаем:

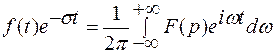или

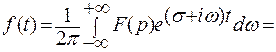
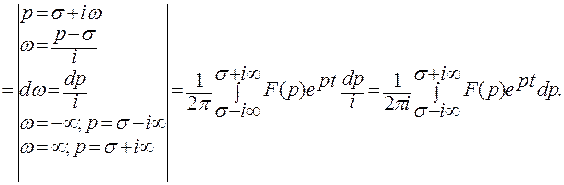
Итак, получим формулу:

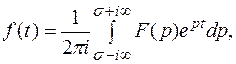(7.1)

где интегрирование производится по любой бесконечной прямой 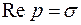, лежащей в полуплоскости абсолютной сходимости интеграла Лапласа (т.е. левее 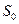) (рис.7.1).

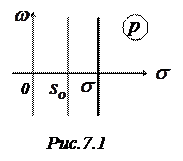
Формула (7.1) является формулой обратного преобразования Лапласа. Еще ее называют формулой Римана-Мелина. Пользуясь этой формулой можно найти оригинал, соответствующий данному изображению. Отметим, что несобственный интеграл, стоящий справа понимается в смысле главного значения

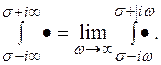
Вычисление интеграла (1) для произвольных аналитических функций F(p) представляет большие трудности, поэтому будем рассматривать важные для нас частные случаи, которые исчерпывают наши потребности в вычислениях f(t).