Параметр оптимизации

Основные понятия и определения теории эксперимента

Общие положения

Большинство научных исследований связано с экспериментом. Он проводится в лабораториях, на производстве, на опытных полях и участках, в клиниках и т. д. Эксперимент может быть физическим, психологическим или модельным. Он может непосредственно проводиться на объекте или на его модели. Модель обычно отличается от объекта масштабом, а иногда природой.

Как вы считаете, можно ли поставить эксперимент на абстрактной математической модели?

Если модель достаточно точно описывает объект, то эксперимент на объекте может быть заменен экспериментом на имитационной модели. В последнее время наряду с физическими моделями все большее распространение получают абстрактные математические модели. Можно получать новые сведения об объекте, экспериментируя на модели, если она достаточно точно описывает объект. Эксперимент занимает центральное место в науке. Однако возникает вопрос, насколько эффективно он используется. Джон Бернал, например, отмечал, что научные исследования организуются и проводятся настолько хаотично, что их коэффициент полезного действия может быть оценен величиной порядка 2%. Для того чтобы повысить эффективность исследований, требуется нечто совершенно новое. Одним из возможных путей является применение математических методов, построение математической теории планирования эксперимента.

Под экспериментом обычно понимают научную постановку опытов с исследуемыми объектами, явлениями или процессами и наблюдение за их характеристиками в строго учитываемых условиях.

Планирование эксперимента — это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью. При этом существенно следующее:

стремление к минимизации общего числа опытов;

одновременное варьирование всеми переменными, определяющими процесс, по специальным правилам — алгоритмам;

использование математического аппарата, формализующего многие действия экспериментатора;

выбор четкой стратегии, позволяющей принимать обоснованные решения после каждой серии экспериментов.

Задачи, для решения которых может использоваться планирование эксперимента, чрезвычайно разнообразны. Поиск оптимальных условий, построение интерполяционных формул, выбор существенных факторов, оценка и уточнение констант теоретических моделей (например, кинетических), выбор наиболее приемлемых из некоторого множества гипотез о механизме явлений, исследование диаграмм состав—свойство — вот примеры задач, при решении которых применяется планирование

эксперимента. Можно сказать, что там, где есть эксперимент, имеет место и наука о его проведении — планирование эксперимента.

В случае применения вычислительных имитационных экспериментов с использованием ЭВМ для исследования свойств систем, требуется предварительная разработка и отладка имитационной модели системы. При ее наличии основная проблема заключается в том, как за конечное время получить достоверную и точную информацию о свойствах системы. Решение этой проблемы немыслимо без планирования имитационного эксперимента. Попутно решают и частные задачи, например, такие как:

снижение затрат машинного времени;

обеспечение точности и достоверности получаемых результатов;

проверка адекватности модели исследуемой системе.

В ходе планирования разрабатывают план имитационного эксперимента, который определяет объем и порядок проведения вычислений на ЭВМ, а также приемы накопления и статистической обработки результатов. Таким образом, при машинном моделировании рационально планировать и проектировать не только саму модельсистемы, но и процесс ее использования, т. е. проведение с ней экспериментов с использованием инструментальной ЭВМ.

При планировании имитационного эксперимента первостепенное значение приобретают:

простота повторения условий эксперимента на ЭВМ с моделью системы;

возможность управления экспериментом с моделью, включая его прерывание и возобновление;

легкость варьирования условий проведения эксперимента (воздействий внешней среды);

наличие корреляции между последовательностью точек в процессе

моделирования;

трудности, связанные с определением интервала моделирования T.

К преимуществам машинных экспериментов относят:

- возможность полного воспроизведения условий эксперимента с моделью исследуемой системы для сравнения двух и более альтернатив;

- простота прерывания и возобновления машинных экспериментов, необходимых для промежуточного анализа результатов и принятия решений об его дальнейшем ходе.

Недостатком машинных экспериментов является наличие корреляции в

выходных последовательностях, т е. результаты одних наблюдений зависят от результатов одного или нескольких предыдущих, и поэтому в них содержится меньше информации, чем в независимых наблюдениях.

Поиск оптимальных условий, как в натурном, так и в модельном эксперименте является одной из наиболее распространенных научно-технических задач. Они возникают в тот момент, когда установлена возможность проведения процесса и необходимо найти наилучшие (оптимальные в некотором смысле) условия его реализации.

Пусть, например, у специалиста возникла гипотеза о том, что при взаимодействии двух веществ должен получаться некоторый интересующий его продукт. Чтобы убедиться в правильности своей гипотезы, он начинает проводить эксперимент. Возможно, что ему повезло, и он получил требуемый продукт. Однако выход продукта весьма низок, скажем, 2%. Вот тут-то и возникает задача выбора оптимальных условий. Требуется так подобрать концентрации реагирующих веществ, температуру, давление, время реакции и другие факторы, чтобы сделать выход возможно более близким к 100%.

В данном примере находятся условия проведения процесса, оптимальные в смысле максимизации выхода требуемого продукта. Но это далеко не единственно возможная постановка задачи. Найденные условия оказались бы другими, если бы ставилась, например, цель минимизации себестоимости продукта или минимизации количества вредных примесей. Следует подчеркнуть, что всегда необходимо четко формулировать, в каком смысле условия должны быть оптимальными. Этим определяется выбор цели исследования. Точная формулировка цели в значительной мере определяет успех исследования.

Задачи, сформулированные аналогичным образом, называются задачами оптимизации. Процесс их решения называется процессом оптимизации или просто оптимизацией. Выбор оптимального состава многокомпонентных смесей или сплавов, повышение производительности действующих установок, повышение качества продукции, снижение затрат на ее получение — вот примеры задач оптимизации.

Чтобы продвинуться дальше, нам придется определить еще ряд важных понятий, первое из которых — объект исследования. Для описания объекта исследования удобно пользоваться моделью черного ящика, который схематически изображен на рисунке 1.1.

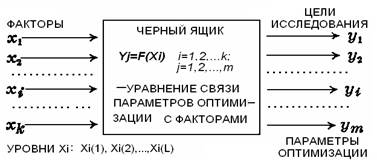
Рисунок 1.1 – Схема черного ящика

Стрелки справа изображают численные характеристики целей исследования (параметров оптимизации), их обозначают буквой yj, j=1,2,…,m. В литературе встречаются и другие названия: критерий оптимизации, целевая функция, выход «черного ящика» и т. д. Для проведения эксперимента необходимо иметь возможность воздействовать на поведение черного ящика. Все способы такого воздействия обозначают буквой xi, i=1,2,…,k и называем факторами. Их называют также входами «черного ящика».

При решении задачи будем использовать математические модели объекта исследования. Под математической моделью мы понимаем уравнение, связывающее параметр оптимизации с факторами. Это уравнение в общем виде можно записать так:

.

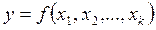Такая функция называется функцией реакции (отклика). Ниже будет рассмотрен вопрос о том, как эту функцию выбрать и построить. А сейчас важно понять, как получаются условия проведения опытов в том эксперименте, который мы собираемся провести. Каждый фактор может принимать в опыте одно из нескольких значений. Такие значения будем называть уровнями. Может оказаться, что фактор способен принимать бесконечно много значений.

Однако на практике точность, с которой устанавливается некоторое значение, не беспредельна. Поэтому будем считать, что всякий фактор имеет определенное число дискретных уровней. Это соглашение существенно облегчает построение «черного ящика» и эксперимента, а также упрощает оценку их сложности.

Фиксированный набор уровней факторов (т. е. установление каждого фактора на некоторый уровень)определяет одно из возможных состояний черного ящика. Одновременно это есть условия проведения одного из возможных опытов. Если перебрать все возможные наборы состояний, то мы получим полное множество различных состояний данного «ящика». Одновременно это будет число возможных различных опытов.

Чтобы узнать число различных состояний, достаточно число уровней факторов L (если оно для всех факторов одинаково) возвести в степень числа факторов k: 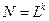. Поупражняйтесь в подсчете числа различных состояний для разных случаев. Это вам пригодится в дальнейшем. Кроме того, реальные объекты, с которыми мы сталкиваемся ежедневно, обладают огромной сложностью. Так, на первый взгляд простая система с пятью факторами на пяти уровнях имеет 3125 состояний, а для десяти факторов на четырех уровнях их уже свыше миллиона! В этих условиях мы просто вынуждены отказаться от таких экспериментов, которые включают все возможные опыты: перебор слишком велик.

Тогда возникает вопрос. Сколько и каких опытов надо включить в эксперимент, чтобы решить поставленную задачу? Здесь-то и приходит на помощь планирование эксперимента. Однако нужно иметь в виду, что при планировании эксперимента не безразлично, какими свойствами обладает объект исследования.

Укажем два основных требования, с которыми приходится считаться.

Прежде всего, существенно, воспроизводятся ли на объекте результаты эксперимента.

Выберем некоторые уровни для всех факторов и в этих условиях проведем эксперимент. Затем повторим его несколько раз через неравные промежутки времени и сравним значения параметра оптимизации. Разброс этих значений характеризует воспроизводимость результатов. Если он не превышает некоторой заранее заданной величины (наших требований к точности эксперимента), то объект удовлетворяет требованию воспроизводимости результатов, а если превышает, то не удовлетворяет этому требованию. Мы будем рассматривать только такие объекты, для которых требование воспроизводимости выполняется.

Планирование эксперимента предполагает активное вмешательство в процесс и возможность выбора в каждом опыте тех уровней факторов, которые представляют интерес. Поэтому такой эксперимент называется активным. Объект, на котором возможен активный эксперимент, называется управляемым. Это и есть второе требование к объекту исследования.

На практике нет абсолютно управляемых объектов. На реальный объект обычно действуют как управляемые, так и неуправляемые факторы. Неуправляемые факторы влияют на воспроизводимость эксперимента и являются причиной ее нарушения. Если требования воспроизводимости не выполняются, приходится обращаться к активно-пассивному эксперименту. Возможно, плохая воспроизводимость объясняется действием фактора, систематически изменяющегося (дрейфующего) во времени. Тогда нужно обращаться к специальным методам планирования .

Наконец, возможно, что все факторы неуправляемы. В этом случае возникает задача установления связи между параметром оптимизации и факторами по результатам наблюдений за поведением объекта, или, как говорят, по результатам пассивного эксперимента.

Таким образом, мы познакомились с основными определениями, которые используются в теории планирования экстремального эксперимента. Прежде чем приступать к эксперименту, необходимо однозначно и непротиворечиво сформулировать его цель и выбрать подходящую количественную характеристику этой цели, которую называют параметром оптимизации. Понятие «объект исследования» требует точного формального определения. Для такого определения подходит модель объекта в виде «черного ящика». Экспериментатор должен уметь формулировать свою задачу в терминах «черного ящика».

Входы «черного ящика» называются факторами. Каждый фактор может принимать некоторое определенное число различных значений, называемых уровнями. Сочетание определенных уровней всех факторов определяет возможное состояние «черного ящика» и условия одного из возможных опытов. Совокупность всех различных возможных состояний определяет сложность «черного ящика» и общее число возможных опытов. Результаты эксперимента используются для получения математической модели объекта исследования, которая представляет собой уравнение, связывающее параметр оптимизации и факторы.

Такое уравнение называется функцией отклика. Использование для получения модели всех возможных опытов приводит к абсурдно большим экспериментам. Задача выбора необходимых для эксперимента опытов, методов математической обработки их результатов и принятия решений — это и есть задача планирования эксперимента. Частный случай этой задачи —

планирование экстремального эксперимента, т.е. эксперимента, поставленного с целью поиска оптимальных условий функционирования объекта. Планирование экстремального эксперимента — метод выбора минимального количества опытов, необходимых для отыскания оптимальных условий.

Параметр оптимизации

В зависимости от объекта и цели исследования параметры оптимизации могут быть весьма разнообразными. Реальные ситуации, как правило, сложны. Они часто требуют одновременного учета нескольких, иногда очень многих, параметров. В принципе каждый объект может характеризоваться сразу всей совокупностью параметров, приведенных на рисунке 1.2, или любым подмножеством из этой совокупности. Движение к оптимуму возможно, если выбран один единственный параметр оптимизации. Тогда прочие характеристики процесса уже не выступают в качестве параметров оптимизации, а служат ограничениями.

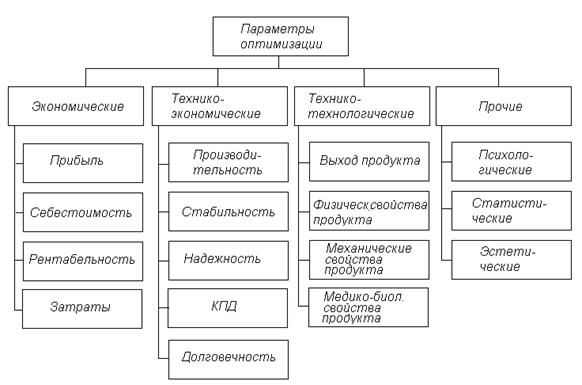
Рисунок 1.2 – Классификация параметров оптимизации

Экономические параметры оптимизации, такие, как прибыль, себестоимость и рентабельность, обычно используются при исследовании действующих промышленных объектов, тогда как затраты на эксперимент имеет смысл оценивать в любых исследованиях, в том числе и лабораторных. Если цена опытов одинакова, затраты на эксперимент пропорциональны числу опытов, которые необходимо поставить для решения данной задачи. Это в значительной мере определяет выбор плана эксперимента.

Среди технико-экономических параметров наибольшее распространение имеет производительность. Такие параметры, как долговечность, надежность и стабильность, связаны с длительными наблюдениями. Имеется некоторый опыт их использования при изучении дорогостоящих ответственных объектов, например радиоэлектронной аппаратуры.

Почти во всех исследованиях приходится учитывать количество и качество получаемого продукта. Как меру количества продукта используют выход, например, процент выхода химической реакции, выход годных изделий. Показатели качества чрезвычайно разнообразны. В нашей схеме они сгруппированы по видам свойств. Характеристики количества и качества продукта образуют группу технико-технологических параметров. Под рубрикой «прочие» сгруппированы различные параметры, которые реже встречаются, но не являются менее важными. Сюда попали статистические параметры, используемые для улучшения характеристик случайных величин или случайных функций.

В качестве примеров назовем задачи на минимизацию дисперсии случайной величины, на уменьшение числа выбросов случайного процесса за фиксированный уровень и т. д. Последняя задача возникает, в частности, при выборе оптимальных настроек автоматических регуляторов или при улучшении свойств нитей (проволока, пряжа, искусственное волокно и др.).

С ростом сложности объекта возрастает роль психологических аспектов взаимодействия человека или животного с объектом. Так, при выборе оптимальной организации рабочего места оператора параметром оптимизации может служить число ошибочных действий в различных возможных ситуациях. Сюда относятся задачи выработки условных рефлексов типа задачи «крысы в лабиринте». При решении задачи технической эстетики или сравнении произведений искусства возникает потребность в эстетической оптимизации. Тогда прочие характеристики процесса уже не выступают в качестве параметров оптимизации, а служат ограничениями.

Требования к параметру оптимизации.Параметр оптимизации — это признак, по которому мы хотим оптимизировать процесс. Он должен быть количественным, задаваться числом. Мы должны уметь его измерять при любой возможной комбинации выбранных уровней факторов. Множество значений, которые может принимать параметр оптимизации, будем называть областью его определения. Области определения могут быть непрерывными и дискретными, ограниченными и неограниченными. Например, выход реакции — это параметр оптимизации с непрерывной ограниченной областью определения. Он может изменяться в интервале от 0 до 100%. Число бракованных изделий, число зерен на шлифе сплава, число кровяных телец в пробе крови — вот примеры параметров с дискретной областью определения, ограниченной снизу.

Уметь измерять параметр оптимизации — это значит располагать подходящим прибором. В ряде случаев такого прибора может не существовать или он слишком дорог. Если нет способа количественного измерения результата, то приходится воспользоваться приемом, называемым ранжированием (ранговым подходом). При этом параметрам оптимизации присваиваются оценки — ранги по заранее выбранной шкале: двухбалльной, пятибалльной и т. д. Ранговый параметр имеет дискретную ограниченную область определения. В простейшем случае область содержит два значения (да, нет; хорошо, плохо). Это может соответствовать, например, годной продукции и браку.

Ранг — это количественная оценка параметра оптимизации, но она носит условный (субъективный) характер. Мы ставим в соответствие качественному признаку некоторое число — ранг. Для каждого физически измеряемого параметра оптимизации можно построить ранговый аналог. Потребность в построении такого аналога возникает, если имеющиеся в распоряжении исследователя численные характеристики неточны или неизвестен способ построения удовлетворительных численных оценок. При

прочих равных условиях всегда нужно отдавать предпочтение физическому измерению, так как ранговый подход менее чувствителен, то с его помощью труднее изучать тонкие эффекты.

Следующее требование: параметр оптимизации должен выражаться одним числом. Иногда это получается естественно, как регистрация показания прибора. Например, скорость движения.

Еще одно требование, связанное с количественной природой параметра оптимизации, — однозначность в статистическом смысле. Заданному набору значений факторов должно соответствовать одно с точностью до ошибки эксперимента значение параметра оптимизации. (Однако обратное неверно: одному и тому же значению параметра могут соответствовать разные наборы значений факторов.) Для успешного достижения цели исследования необходимо, чтобы параметр оптимизации действительно оценивал эффективность функционирования системы в заранее выбранном смысле.

Это требование является главным, определяющим корректность постановки задачи. Представление об эффективности не остается постоянным в ходе исследования. Оно меняется по мере накопления информации и в зависимости от достигнутых результатов. Это приводит к последовательному подходу при выборе параметра оптимизации.

Так, например, на первых стадиях исследования технологических процессов в качестве параметра оптимизации часто используется выход продукта. Однако в дальнейшем, когда возможность повышения выхода исчерпана, нас начинают интересовать такие параметры, как себестоимость, чистота продукта и т. д. Говоря об оценке эффективности функционирования системы, важно помнить, что речь идет о системе в целом. Часто система состоит из ряда подсистем, каждая из которых может оцениваться своим локальным параметром оптимизации.

При этом оптимальность каждой из подсистем по своему параметру оптимизации «не исключает возможности гибели системы в целом» [6]. Мало иметь эффективный параметр оптимизации. Надо еще, чтобы он был эффективный в статистическом смысле. Фактически это требование сводится к выбору параметра оптимизации, который определяется с наибольшей возможной точностью. Если и эта точность недостаточна, тогда приходится обращаться к увеличению числа повторных опытов.

Пусть, например, нас интересует исследование прочностных характеристик некоторого сплава. В качестве меры прочности можно использовать как прочность на разрыв, так и макротвердость. Поскольку эти характеристики функционально связаны, то с точки зрения эффективности они эквивалентны. Однако точность измерения первой характеристики существенно выше, чем второй. Требование статистической эффективности заставляет отдать предпочтение прочности на разрыв.

Следующее требование к параметру оптимизации — требование универсальности или полноты. Под универсальностью параметра оптимизации понимается его способность всесторонне характеризовать объект. В частности, технологические параметры оптимизации недостаточно универсальны: они не учитывают экономику. Универсальностью обладают, например, обобщенные параметры оптимизации, которые строятся как функции от нескольких частных параметров [1].

Пример выбора параметра оптимизации, обладающего полнотой, рассмотрен в работе [1] для процессов зонной перекристаллизации. Применяемый для этой цели коэффициент распределения, представляющий отношение концентраций примесей в твердой и жидкой фазах, излишне специфичен. Предложен более полный параметр оптимизации — энтропийная функция S:

,

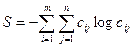где 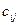— концентрация i-той примеси (при их числе m) в j-м участке слитка (при их числе n).

Желательно, чтобы параметр оптимизации имел физический смысл, был простым и легко вычисляемым. Требование физического смысла связано с последующей интерпретацией результатов эксперимента. Не представляет труда объяснить, что значит максимум извлечения, максимум содержания ценного компонента. Эти и подобные им технологические параметры оптимизации имеют ясный физический смысл, но иногда для них может не выполняться, например, требование статистической эффективности. Тогда рекомендуется переходить к преобразованию параметра оптимизации.

Второе требование часто также оказывается весьма существенным. Для процессов разделения термодинамические параметры оптимизации более универсальны. Однако на практике ими пользуются мало: их расчет довольно труден. Пожалуй, из этих двух требований первое является более существенным, потому что часто удается найти идеальную характеристику системы и сравнить ее с реальной характеристикой. Иногда при этом целесообразно нормировать параметр с тем, чтобы он принимал значения от нуля до единицы.

Кроме высказанных требований и пожеланий при выборе параметра оптимизации нужно еще иметь в виду, что параметр оптимизации в некоторой степени оказывает влияние на вид математической модели исследуемого объекта.

Экономические параметры, в силу их аддитивной природы, легче представляются простыми функциями, чем физико-химические показатели. Не случайно методы линейного программирования, основанные на простых моделях, получили широкое распространение именно в экономике. Температура плавления сплава является, как известно, сложной, многоэкстремальной характеристикой состава, тогда как стоимость сплава зависит от состава линейно.

Задачи с одним выходным параметромимеют очевидные преимущества. Но на практике чаще всего приходится учитывать несколько выходных параметров. Иногда их число довольно велико. Так, например, при производстве резиновых и пластмассовых изделий приходится учитывать физико-механические, технологические, экономические, художественно-эстетические и другие параметры (прочность, эластичность, относительное удлинение, способность смеси прилипать к форме и т. д.). Математические модели можно построить для каждого из параметров, но одновременно оптимизировать несколько функций невозможно.

Обычно оптимизируется одна функция, наиболее важная с точки зрения цели исследования, при ограничениях, налагаемых другими функциями. Поэтому из многих выходных параметров выбирается один в качестве параметра оптимизации, а остальные служат ограничениями. Всегда полезно исследовать возможность уменьшения числа выходных параметров.

Для этого можно воспользоваться корреляционным анализом. При этом между всевозможными парами параметров необходимо вычислить коэффициент парной корреляции, который является общепринятой в математической статистике характеристикой связи между двумя случайными величинами. Если обозначить один параметр через y1 а другой — через у2, и число опытов, в которых они будут измеряться, — через N, так, что u=1, 2, . . ., N, где u — текущий номер опыта, то коэффициент парной корреляции 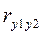вычисляется по формуле:

.

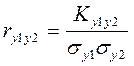Значения коэффициента парной корреляции могут лежать в пределах от —1 до +1. Если с ростом значения одного параметра возрастает значение другого, у коэффициента будет знак плюс, а если уменьшается, то минус. Чем ближе найденное значение 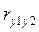к единице, тем сильнее значение одного параметра зависит от того, какое значение принимает другой, т. е. между такими параметрами существует линейная связь, и при изучении процесса можно рассматривать только один из них. Необходимо помнить, что коэффициент парной корреляции как мера тесноты связи имеет четкий математический смысл только при линейной зависимости между параметрами и в случае нормального их распределения.

Для проверки значимости коэффициента парной корреляции нужно сравнить его значение с табличным (критическим) значением 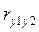, которое приводится в таблице критических значений. Для пользования этой таблицей нужно знать число степеней свободы f=N-2 и выбрать определенный уровень значимости, например, равный 0,05. Такое значение уровня значимости называют еще 5%-ным уровнем риска, что соответствует вероятности верного ответа "при проверке нашей гипотезы P=1- а=0,95, или 95%.

Это значит, что в среднем только в 5% случаев возможна ошибка при проверке гипотезы. В практических исследованиях 5%-ный уровень риска применяется наиболее часто. Но экспериментатор всегда свободен в выборе уровня значимости, и возможны ситуации, в которых, например, требуется однопроцентный уровень риска. При этом возрастает надежность ответа. Проверка гипотезы сводится к сравнению абсолютной величины коэффициента парной корреляции с критическим значением. Если экспериментально найденное значение 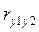меньше критического, то нет оснований считать, что имеется тесная линейная связь между параметрами, а если больше или равно, то гипотеза о корреляционной линейной связи не отвергается [4].

При высокой значимости коэффициента корреляции любой из двух анализируемых параметров можно исключить из рассмотрения как не содержащий дополнительной информации об объекте исследования. Исключить можно тот параметр, который технически труднее измерять, или тот, физический смысл которого менее ясен. При планировании эксперимента целесообразно измерять все параметры, затем оценить корреляцию между ними и строить модели для их минимально возможного числа или же воспользоваться обобщенным параметром. Но бывают случаи, когда приходится рассматривать и коррелированные параметры.

Таким образом, параметр оптимизации — это реакция (отклик) на воздействия факторов, которые определяют поведение изучаемой системы.

Параметры оптимизации бывают экономическими, технико-экономическими, технико-технологическими, статистическими, психологическими и т. д.

Параметр оптимизации должен:

- быть эффективным с точки зрения достижения цели;

- быть универсальным;

- быть количественным и выражаться одним числом;

- быть статистически эффективным;

- иметь физический смысл, быть простым и легко вычисляемым;

- существовать для всех различимых состояний.

В тех случаях, когда возникают трудности с количественной оценкой параметров оптимизации, приходится обращаться к ранговому подходу. В ходе исследования могут меняться априорные представления об объекте исследования, что приводит к последовательному подходу при выборе параметра оптимизации.

Из многих параметров, характеризующих объект исследования, только один, часто обобщенный, может служить параметром оптимизации. Остальные рассматриваются как ограничения.

Построение обобщенного параметра оптимизации связано с созданием единого признака, количественно определяющего функционирование исследуемого объекта с многими выходными параметрами. При этом возникают некоторые трудности. Каждый выходной параметр—отклик—имеет свой физический смысл, свою размерность. Чтобы объединить различные отклики, необходимо ввести единую для всех откликов искусственную метрику.

Набор данных каждого отклика нужно поставить в соответствие с некоторым стандартным аналогом, с безразмерной шкалой. Поэтому первым вопросом, который нужно решить при построении обобщенного параметра оптимизации, является вопрос о выборе шкалы. Шкала должна быть однотипной для всех объединяемых откликов. Построение шкалы во многом зависит от уровня априорных сведений о выходных параметрах, а также от той точности, с которой мы хотим определить обобщенный отклик.

Второй важный вопрос — выбор правила комбинирования исходных частных откликов в обобщённый показатель. Единого правила не существует, здесь можно идти различными путями, и выбор пути не формализован.

Факторы

После того как выбран объект исследования и параметр оптимизации, нужно включить в рассмотрение все существенные факторы, которые могут влиять на процесс. Если какой-либо существенный фактор окажется неучтенным, то это может привести к неприятным последствиям. Так, если неучтенный фактор произвольно флуктуировал — принимал случайные значения, которые экспериментатор не контролировал, — это значительно увеличит ошибку опыта.

Рассмотрим процесс планирования эксперимента применительно к такой цели моделирования как отыскание функциональной зависимости между переменными модели. В зависимости от своей роли каждая переменная может быть либо фактором, либо реакцией. Если изучается влияние переменной x на переменную y, то x – фактор, а y – реакция.

Каждый фактор может принимать в опыте одно из нескольких значений. Такие значения будем называть уровнями. Может оказаться, что фактор способен принимать бесконечно много значений (непрерывный ряд). Однако на практике точность, с которой устанавливается некоторое значение, не беспредельна. Поэтому мы вправе считать, что всякий фактор имеет определенное число дискретных уровней. Это соглашение существенно облегчает построение «черного ящика» и эксперимента, а также упрощает оценку их сложности.

Каждый из факторов имеет верхний и нижний уровни, расположенные симметрично относительно некоторого нулевого уровня. Точка в факторном пространстве, соответствующая нулевым уровням всех факторов, называется центром плана. Интервалом варьирования фактора называется некоторое число J, прибавление которого к нулевому уровню дает верхний уровень, а вычитание – нижний.

Фиксированный набор уровней факторов в одном из опытов эксперимента представляет собой лишь одну комбинацию уровней факторов, которая определяет одно из возможных состояний системы. Каждому фиксированному набору уровней факторов соответствует точка в многомерном пространстве, называемом факторным пространством. Из-за временных ограничений эксперимент выполняют не во всех точках факторного пространства, а лишь в точках допустимой области, что показано для случая двух факторов x1 и x2 на рис.1.3 (плоскость x10x2).

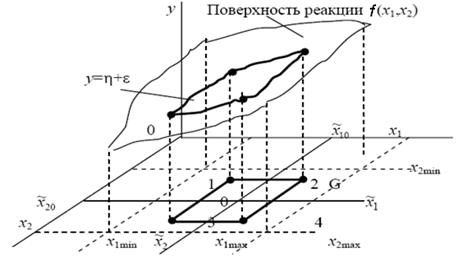
Рисунок 1.3 – Геометрическое представление поверхности реакции

Для этого находят минимальное число испытаний (число точек факторного пространства), которое обеспечивает выявление функциональной зависимости:

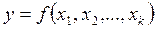
с требуемой точностью и достоверностью.

При поддержании фактора на некотором фиксированном уровне может быть получено ложное представление об оптимуме, так как нет гарантии, что фиксированный уровень является оптимальным. Как же преодолеть большое число опытов? Чем больше факторов, тем больше опытов». Действительно, число опытов растет по показательной функции. Размерность факторного пространства увеличивается, и математики в таких случаях говорят о «проклятии размерности». Рекомендации о том, как преодолеть «проклятие размерности», вы найдете ниже.

Если число факторов больше пятнадцати, нужно обратиться к методам отсеивания несущественных факторов. Здесь можно воспользоваться формализацией априорной информации [1], методом случайного баланса, планами Плаккета-Бермана и др. Иногда эти планы применяются и при меньшем числе факторов.

Определение фактора. Фактором называется измеряемая переменная величина, принимающая в некоторый момент времени определенное значение. Факторы соответствуют способам воздействия на объект исследования. Так же, как и параметр оптимизации, каждый фактор имеет область определения. Мы будем считать фактор заданным, если вместе с его названием указана область его определения.

Под областью определения понимается совокупность всех значений, которые в принципе может принимать данный фактор. Ясно, что совокупность значений фактора, которая используется в эксперименте, является подмножеством из множества значений, образующих область определения. Область определения может быть непрерывной и дискретной. Однако в тех задачах планирования эксперимента, которые мы собираемся рассматривать, всегда используются дискретные области определения. Так, для факторов с непрерывной областью определения, таких, как температура, время, количество вещества и т. п., всегда выбираются дискретные множества уровней.

В практических задачах области определения факторов, как правило, ограничены. Ограничения могут носить принципиальный либо технический характер. Произведем классификацию факторов в зависимости от того, является ли фактор переменной величиной, которую можно оценивать количественно: измерять, взвешивать, титровать и т. п., или же он — некоторая переменная, характеризующаяся качественными свойствами.

По этому признаку факторы делят на количественные и качественные. Качественные факторы — это разные вещества, разные технологические способы, аппараты, исполнители и