Анкета для сбора априорной информации
Постановка задачи, выбор параметров оптимизации
1. Краткое описание процесса, объекта.
2. Формулировка цели исследования (если задач несколько, то ранжирование их по степени важности).
3. Выбор параметров оптимизации (откликов).
Заполните таблицу 2.1, включив в нее все возможные отклики.
Таблица 2.1 – Перечень параметров оптимизации
| Номер отклика | Название | Размерность | Область определения | Точность | Примечание |
4. Желаемый результат. Число и точность.
5. Какой результат будет считаться отличным, хорошим,
удовлетворительным, неудовлетворительным.
Выбор факторов
1. Список всех «подозреваемых»: факторов, которые могут влиять на процесс.
2. Список факторов, включаемых в реальный эксперимент (таблица 2.2).
Таблица 2.2 – Список факторов
| Номер фактора | Название | Размерность | Область определения | Точность | Примечание |
3. Существуют ли возможности установления значения фактора на любом заданном уровне?
4. Сохраняются ли заданные значения уровней в течение опыта?
5. Могут ли некоторые комбинации уровней факторов привести к остановке процесса (например, взрыв, не технологичность и т. д.)?
Число опытов
1. Желаемое число опытов, ограничения на число опытов.
2. Желаемый срок проведения исследования.
3. Примерная длительность одного опыта.
4. Стоимость и затраты труда при проведении одного опыта, серии.
5. Желаемое число уровней для одного фактора.
6. Возможность выполнения параллельных опытов и их желаемое число.
7. Возможность проведения параллельных измерений.
8. Желаемая стратегия проведения опытов (например, по одному в день и т. д.).
Учет априорной информации
1. Условия и результаты, достигнутые при изучении аналогичных процессов.
2. Результаты предварительного эксперимента и данные (литературные и собственные) о величине ошибки эксперимента.
3. Взаимодействия факторов.
В следующем параграфе приведен конкретный пример постановки задачи, в котором использованы некоторые части этой анкеты.
2.2 Реализация плана эксперимента
К проведению опытов необходимо тщательно подготовиться, собрать опытную установку, проверить и прокалибровать приборы, подготовить исходное сырье, составить специальный журнал.
Журнал заранее оформляют в соответствии с методикой и планом опытов так, чтобы была ясна последовательность действий. Первую страницу можно посвятить выбору цели исследования и параметрам оптимизации, с указанием их размерностей.
Желательно перечислить все параметры, которые могут служить характеристиками процесса и указать, какая между ними существует корреляция. Если же сведения о корреляции отсутствуют, целесообразно подсчитать коэффициенты парной корреляции, проверить их значимость и выделить группу некоррелированных параметров. На второй странице перечислить факторы и поместить таблицу уровней факторов и интервалов варьирования. Не забудьте указать единицы измерения факторов!
Для матрицы планирования удобно отвести разворот журнала, чтобы имелась возможность дополнить ее до расчетной матрицы, записать повторные опыты и примечания.
Чтобы облегчить работу лаборанта и исключить ошибки, связанные с
выбором условий опыта, в рабочей матрице планирования целесообразно проставлять не только кодовые значения факторов, но и натуральные.
При составлении рабочей матрицы планирования необходимо оставить место для столбцов, в которых отмечаются даты постановки опытов и фамилии лаборантов, если опыты проводят несколько человек. Имея перед собой план опытов, необходимо подсчитать количество исходного сырья и заранее его подготовить.
Желательно, чтобы сырье было однородное. Если требование однородности выполнить невозможно, нужно заблаговременно определить количество различных партий сырья и соответствующим образом разбить матрицу планирования на блоки.
На этом вопросе мы далее остановимся подробно. Отдельные страницы нужно отвести для расчетов, которые необходимы для определения количества всех компонентов отклика и т. п., а также для анализа результатов эксперимента. Все расчеты должны сохраняться до окончания работы.
Пример 1. В качестве примера приводится оформление журнала при оптимизации исследуемого процесса.
Планирование эксперимента при оптимизации процесса.
Цель исследования: определение оптимальных условий процесса.
Параметры, характеризующие процесс:
Формулировка задачи оптимизации.
Факторы, определяющие процесс.
Выбор варьируемых факторов. Принятие решения по выбору числа управляемых факторов в опытах.
Выбор технологии.
Описание экспериментальной установки. Опыты проводятся на лабораторной установке (описание установки).
Выбор основного уровня и интервалов варьирования. Для того чтобы
выбрать уровни факторов, следует собрать и проанализировать литературные и данные ранее проведенных испытаний.
На основании анализа имеющихся сведений решено выбрать следующие уровни и интервалы варьирования факторов таблице 2.3.
Таблица 2.3 – Уровни факторов и интервалы варьирования
| Факторы | Уровни | I | Размерность | ||
| -1 | +1 | ||||
| x1 | час | ||||
| x2 | % | ||||
| x3 | % |
Имея такую таблицу, можно приступить к обработке экспериментальных данных. Каждая горизонтальная строка матрицы — это условия опыта. Условия опытов чрезвычайно разнообразны. Ведь мы занимаемся планированием многофакторного эксперимента, когда все факторы изменяются одновременно (таблица 2.4).
Таблица 2.4 – Матрица планирования и результаты эксперимента
| Номер опыта | СЧ | Дата | x1 | x2 | x3 | y1, % | ||||
| код | час | код | % | код | % | Повтор | Среднее | |||
| 10.03 | - | - | - | 80,23 | 81,08 | |||||
| 5.04 | 81,93 | |||||||||
| 21.03 | + | - | - | 86,50 | 85,65 | |||||
| 14.04 | 84,80 | |||||||||
| 8.03 | - | + | - | 82,45 | 82,27 | |||||
| 21.04 | 82,10 | |||||||||
| 27.03 | + | + | - | 89,50 | 90,40 | |||||
| 6.04 | 91,30 | |||||||||
| 12.03 | - | - | + | 85,10 | 84,95 | |||||
| 27.04 | 84,80 | |||||||||
| 1.04 | + | - | + | 90,30 | 89,95 | |||||
| 16.04 | 89,60 | |||||||||
| 15.03 | - | + | + | 85,60 | 88,25 | |||||
| 12.04 | 84,90 | |||||||||
| 20.03 | + | + | + | 88,02 | 88,25 | |||||
| 9.04 | 88,48 |
Приступая к планированию эксперимента, мы должны отказаться oт использования классического эксперимента, который применим в основном для исследования систем, у которых, как правило, отсутствует взаимное влияние факторов. В сложных системах обычно наблюдается взаимодействие факторов, что существенно затрудняет выявление истинных связей между реакцией и факторами методом изменения факторов по одному.
Проанализируем, в чем состоит недостаток однофакторного эксперимента и почему им нецелесообразно пользоваться при исследовании многофакторных систем. При однофакторном эксперименте, варьируя одним фактором и стабилизируя все прочие на произвольно выбранных уровнях, экспериментатор получает зависимость параметра оптимизации только от одного фактора и определяет локальный оптимум. Далее он повторяет аналогичную процедуру для второго, третьего и k-то фактора.
В результате длительной и кропотливой работы, требующей много средств и времени, опытные данные представляются десятками графиков, которые, в сущности, имеют иллюстративный характер.
За время эксперимента могут происходить изменения в аппаратуре, сырье и т. д. Все это вносит изменения в результаты эксперимента, вследствие чего данные многих опытов являются несопоставимыми. В планировании эксперимента разработана четкая стратегия экспериментирования. Экспериментатор может минимизировать число опытов, пользуясь шаговым принципом и дробным планированием.
Имеются способы борьбы с неконтролируемым дрейфом, вызванным изменением аппаратуры, сырья и т. п., которые не предусмотрены в однофакторном эксперименте.
Проанализируем применение однофакторного эксперимента при исследовании системы с семью факторами. Итак, экспериментатору необходимо исследовать влияние семи факторов на некоторый параметр оптимизации и он решил проводить однофакторный эксперимент. Для того чтобы построить кривую, обычно берут четыре-пять экспериментальных точек. Возьмем четыре точки. Необходимое количество опытов при реализации всевозможных комбинаций равно N=4^7=16384. Совершенно ясно, что такое количество опытов реализовать невозможно. Значит, экспериментатор произвольно отбросит очень многие комбинации и реализует небольшую часть опытов, изменяя факторы по одному при постоянных значениях прочих факторов. Тогда естественно возникнет вопрос, как будут выглядеть кривые, если прочие факторы стабилизировать на другом уровне? Несомненно, кривые изменятся. Перебрать все комбинации — значит поставить 16384 опыта.
Рассмотренный ранее шаговый принцип исследования поверхности отклика и дробный факторный эксперимент предлагают экспериментатору разумный путь минимизации числа опытов.
В процессе реализации матрицы планирования (таблица 2.4) получают результаты эксперимента, например, в виде значений отклика y1.
Одновременное изменение всех факторов вносит в условия опытов большое разнообразие. Разнообразие увеличивается с ростом числа факторов. Но всегда ли легко определить, что один опыт лучше другого? Неправильно утверждать, что условия одного опыта более выгодны с точки зрения величины параметра оптимизации, чем другого опыта.
Экспериментаторы, вооруженные статистическими методами, поступают осторожно. Они должны проверить, значимо ли отличаются результаты опытов друг от друга. Интуитивное мнение является чрезвычайно слабым указанием на возможное превосходство какого-либо одного опыта. Нужны объективные оценки. Прежде всего, должна быть известна ошибка опыта, которая может быть столь большой, что разница в выходе потонет на ее фоне. И, напротив, ошибка может иметь столь малую величину, что разница в 2,1% окажется значимой. Если известна ошибка опыта, то значимость различий двух средних можно проверить с помощью t-критерия (критерия Стьюдента) по формуле:
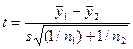 ,
,
где 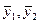 — среднее значение выходного параметра в одном опыте и среднее
— среднее значение выходного параметра в одном опыте и среднее
значение выходного параметра в другом опыте соответственно, s — ошибка опыта (рассматривается случай, когда ошибки для первого и второго опыта близки одна к другой), n1 — количество наблюдений в первом опыте, n2 — количество наблюдений во втором опыте.
Эта формула предназначена для сравнения средних значений двух малых выборок с равными дисперсиями. Проверка значимости ведется по табулированным значениям t-критерия. Так, если в нашем случае s=1, количество параллельных опытов одинаково и равно двум, то
t = 2,1/1*(0,5+0,5)^0,5 = 2,1.
Число степеней свободы равно f=n1+n2—2=2. Табличное значение t-критерия для f=2 и 5%-ного уровня значимости равно 4,3. Это означает, что вероятность того, что при 2 степенях свободы, значение величины t будет больше по абсолютной величине, чем 4,3, равна 0,05. Поскольку экспериментальное значение t меньше табличного, то с вероятностью Р=1 — а=0,95 можно считать, что разницы между результатами двух опытов нет. А теперь познакомимся с вычислением ошибки опыта, или, как ее часто называют, ошибки воспроизводимости.
Дата добавления: 2021-11-16; просмотров: 636;











