А параметр этого потока
lm = l/(m + 1). (2.18)
Из (2.17) и (2.18) следует, что с увеличение порядка Эрланга увеличивается математическое ожидание и дисперсия промежутка времени между заявками и одновременно уменьшается параметр потока. Потоки Эрланга m-го порядка при разных m создают потоки с различной степенью случайности: от простейшего (m = 0) до детерминированного (m = ¥).
Неоднородный входящий поток
Как уже отмечалось, в неоднородном потоке каждая заявка имеет две и более характеристики. Рассмотрим модели неоднородных потоков, когда в качестве второй характеристики используются требования входящей заявки на число обслуживающих приборов.
Входной поток представим как композицию пуассоновских однородных потоков, каждый из которых требует для своего обслуживания определенное (фиксированное) число обслуживающих приборов. При этом число однородных пуассоновских потоков L = qmax – qmin + 1, а интенсивность каждого m-го потока (m Î L) lm = P(m) lS, где qmax и qmin – максимальное и минимальное значение обслуживающих приборов, требуемых заявками; P(m) – вероятность запроса m обслуживающих приборов (для общности получаемых результатов распределение запросов будем полагать произвольным, а в качестве примера рассмотрим равномерное распределение, т.е. P(m) = P(k) = 1/(qmax – qmin+ 1), k, m Î L [11]).
Рассмотрим предлагаемую модель. Пусть k – количество потоков заявок, а n – количество источников, которые являются неоднородными, причем i-й источник участвует в образовании Mi потоков (i Î 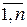 ). Входной поток lå может быть описан следующим образом (табл. 2.1).
). Входной поток lå может быть описан следующим образом (табл. 2.1).
Таблица 2.1
| Число источников | Число каналов | |||||
| qmin | … | qi | … | qmax(k) | N | |
| λ11 | … | λ1i | … | λ1k | N1 | |
| … | … | … | … | … | … | … |
| i | λi1 | … | λii | … | λik | Ni |
| … | … | … | … | … | … | … |
| k | λk1 | … | λki | … | λkk | Nk |
Здесь lij – константы, определяющие интенсивность в i-м потоке с требованиями на j каналов; Ni – количество источников заявок в потоке i-го типа.
Некоторые lij = 0, но в строке i должно быть Mi ненулевых компонентов. Модель такого типа называется мультивекторной [11].
Ниже приводится матричная [12] модель неоднородного входного потока с более наглядной формой задания, эквивалентная мультивекторной модели. Рассмотрим особенности матричной модели неоднородного потока заявок. Этот поток формируется n неодинаковыми и неоднородными источниками, каждый из которых с интенсивностью lji генерирует i-за-явки, 1 £ i £ k. Неоднородный поток матричной модели характеризуется матрицей
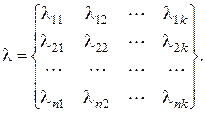
Здесь при 1 £ j £ n, 1 £ i £ k, lji – интенсивность потока i-заявок от j-го источника.
Если в матричной модели n = N1 + N2 + … + Nk, а в мультивекторной модели строки с номерами 1 … N1 одинаковы и совпадают с вектором 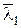 , строки с номерами 1 … N2 одинаковы и совпадают с вектором
, строки с номерами 1 … N2 одинаковы и совпадают с вектором 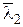 , и т.д., то матричная модель порождает мультивекторную модель неоднородного потока. Верно и обратное утверждение. Если в мультивекторной модели k = = n, а все Nj = 1, то мультивекторная модель порождает матричную, т.е. эти две модели эквивалентны.
, и т.д., то матричная модель порождает мультивекторную модель неоднородного потока. Верно и обратное утверждение. Если в мультивекторной модели k = = n, а все Nj = 1, то мультивекторная модель порождает матричную, т.е. эти две модели эквивалентны.
Рассмотренные модели неоднородных входных потоков обеспечивают описание реальных процессов в аналого-цифровых преобразователях (АЦП), системах телекоммуникаций, информационно-измерительных системах (ИИС), автоматических системах управления технологическими процессами (АСУТП), автоматических системах научных исследований (АСНИ), системах автоматизации испытаний (САИ). Мультивекторные и матричные модели представляют обобщенное описание неоднородных потоков, инвариантное к областям применения. Очевидное достоинство матричной модели – это простота ее описания и исследования. А достоинством мультивекторной модели является явное использование ею специфики матрицы, когда в ней встречается много совпадающих строк, что существенно понижает размерность множества состояний соответствующих СМО.
Дата добавления: 2021-01-11; просмотров: 917;











