Полный факторный эксперимент и математическая модель
Давайте еще раз вернемся к матрице 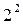 (таблица 2.4). Для движения к точке оптимума нам нужна линейная модель
(таблица 2.4). Для движения к точке оптимума нам нужна линейная модель 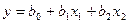 . Наша цель — найти по результатам эксперимента значения неизвестных коэффициентов модели. До сих пор, говоря о линейной модели, мы не останавливались на важном вопросе о статистической оценке ее коэффициентов. Теперь необходимо сделать ряд замечаний по этому поводу. Можно утверждать, что эксперимент проводится для проверки гипотезы о том, что линейная модель
. Наша цель — найти по результатам эксперимента значения неизвестных коэффициентов модели. До сих пор, говоря о линейной модели, мы не останавливались на важном вопросе о статистической оценке ее коэффициентов. Теперь необходимо сделать ряд замечаний по этому поводу. Можно утверждать, что эксперимент проводится для проверки гипотезы о том, что линейная модель 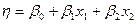 адекватна. Греческие буквы использованы для обозначения «истинных» генеральных значений соответствующих неизвестных. Эксперимент, содержащий конечное число опытов, позволяет только получить выборочные оценки для коэффициентов уравнения:
адекватна. Греческие буквы использованы для обозначения «истинных» генеральных значений соответствующих неизвестных. Эксперимент, содержащий конечное число опытов, позволяет только получить выборочные оценки для коэффициентов уравнения:
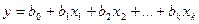 .
.
Их точность и надежность зависят от свойств выборки и нуждаются в статистической проверке. Как производится такая проверка, вы узнаете ниже. А пока займемся вычислением оценок коэффициентов. Их можно вычислить формуле, обоснование которой дается ниже:
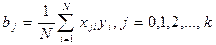 .
.
Воспользуемся этой формулой для подсчета коэффициентов b1 и b2.
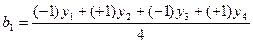 ,
, 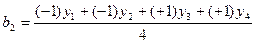 .
.
Вы видите, что благодаря кодированию факторов расчет коэффициентов превратился в простую арифметическую процедуру. Для подсчета коэффициента b1 используется вектор-столбец x1 а для b2 — столбец x2. Остается неясным, как найти b0. Если наше уравнение 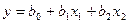 справедливо, то оно верно и для средних арифметических значений переменных:
справедливо, то оно верно и для средних арифметических значений переменных: 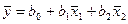 . Но в силу свойства симметрии
. Но в силу свойства симметрии 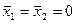 . Следовательно,
. Следовательно, 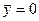 . Откуда bо есть среднее арифметическое значение параметра оптимизации. Чтобы его получить, необходимо сложить все значения y и сумму разделить на число опытов. Чтобы привести эту процедуру в соответствие с формулой для вычисления коэффициентов, в матрицу планирования удобно ввести вектор-столбец фиктивной переменной xo, которая принимает во всех опытах значение +1. Это было уже учтено в записи формулы, где j принимало значения от 0 до k. Теперь у нас есть все необходимое, чтобы найти неизвестные коэффициенты линейной модели
. Откуда bо есть среднее арифметическое значение параметра оптимизации. Чтобы его получить, необходимо сложить все значения y и сумму разделить на число опытов. Чтобы привести эту процедуру в соответствие с формулой для вычисления коэффициентов, в матрицу планирования удобно ввести вектор-столбец фиктивной переменной xo, которая принимает во всех опытах значение +1. Это было уже учтено в записи формулы, где j принимало значения от 0 до k. Теперь у нас есть все необходимое, чтобы найти неизвестные коэффициенты линейной модели 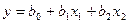 .
.
Коэффициенты при независимых переменных указывают на силу влияния факторов. Чем больше численная величина коэффициента, тем большее влияние оказывает фактор. Если коэффициент имеет знак плюс, то с увеличением значения фактора параметр оптимизации увеличивается, а если минус, то уменьшается. Величина коэффициента соответствует вкладу данного фактора в величину параметра оптимизации при переходе фактора с нулевого уровня на верхний или нижний. Иногда удобно оценивать вклад фактора при переходе его от нижнего к верхнему уровню. Вклад, определенный таким образом, называется эффектом фактора (иногда его называют основным или главным эффектом). Он численно равен удвоенному коэффициенту. Для качественных факторов, варьируемых на двух уровнях, основной уровень не имеет физического смысла. Поэтому понятие «эффект фактора» является здесь естественным. Планируя эксперимент, на первом этапе стремятся получить линейную модель. Однако при этом нет гарантии, что в выбранных интервалах варьирования процесс описывается линейной моделью. Существуют способы проверки пригодности линейной модели (проверка адекватности — см. гл. 9). А если модель нелинейна, как количественно оценить нелинейность, пользуясь полным факторным экспериментом?
Один из часто встречающихся видов нелинейности связан с тем, что эффект одного фактора зависит от уровня, на котором находится другой фактор. В этом случае говорят, что имеет место эффект взаимодействия двух факторов. Полный факторный эксперимент позволяет количественно оценивать эффекты взаимодействия. Для этого надо, пользуясь правилом перемножения столбцов, получить столбец произведения двух факторов. При вычислении коэффициента, соответствующего эффекту взаимодействия с новым вектор-столбцом можно обращаться так же, как с вектор-столбцом любого фактора. Для полного факторного эксперимента 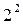 матрица планирования с учетом эффекта взаимодействия представлена в таблице 1.7. Очень важно, что при добавлении столбцов эффектов взаимодействий все рассмотренные свойства матриц планирования сохраняются.
матрица планирования с учетом эффекта взаимодействия представлена в таблице 1.7. Очень важно, что при добавлении столбцов эффектов взаимодействий все рассмотренные свойства матриц планирования сохраняются.
Таблица 1.7- Матрица планирования эксперимента 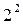 с эффектом взаимодействия
с эффектом взаимодействия
| Номер опыта | X0 | X1 | X2 | X1X2 | Y | Номер опыта | X0 | X1 | X2 | X1X2 | Y |
| +1 | +1 | +1 | +1 | Y1 | +1 | -1 | -1 | +1 | Y3 | ||
| +1 | -1 | +1 | -1 | Y2 | +1 | +1 | -1 | -1 | Y4 |
Теперь модель выглядит следующим образом:
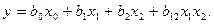
Коэффициент b12 вычисляется обычным путем
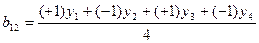 .
. 
Столбцы x1 и х2 задают планирование — по ним непосредственно
определяются условия опытов, а столбцы х0 и x1x2 служат только для расчета. Обращаем ваше внимание на то, что при оптимизации мы стремимся сделать эффекты взаимодействия возможно меньшими. В задачах интерполяции, напротив, их выявление часто важно и интересно.
Пример расчета коэффициентов по результатам эксперимента приведен в таблице 1.8.
Таблица 1.8 – Расчетная матрица и результаты 
| Номер опыта | X0 | X1 | X2 | X1X2 | Буквенные обозначения строк | Y |
| +1 | -1 | -1 | +1 | (1) | ||
| +1 | +1 | -1 | -1 | a | ||
| +1 | -1 | +1 | -1 | b | ||
| +1 | +1 | +1 | +1 | ab |
Обратите внимание на то, что порядок коэффициентов в последнем столбце соответствует порядку буквенных обозначений матрицы планирования (рисунок 1.18). Так, строке (1) соответствует bо, строке (а) — b1 и т. д. Порядок буквенных обозначений зависит от порядка опытов, который должен быть фиксированным.
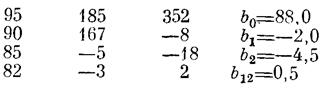
Рисунок 1.18 - Результаты расчета коэффициентов
С ростом числа факторов число возможных взаимодействий быстро растет. Мы рассмотрели самый простой случай, когда имелось одно взаимодействие. Обратимся теперь к полному факторному эксперименту 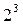 .
.
Матрица планирования 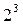 с учетом всех возможных взаимодействий приведена в таблице 1.9.
с учетом всех возможных взаимодействий приведена в таблице 1.9.
Таблица 1.9 – Полный факторный эксперимент 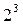
| Номер опыта | X0 | X1 | X2 | X3 | X1X2 | X1X3 | X2X3 | X1X2X3 | Y |
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | Y1 | |
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | Y2 | |
| +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | Y3 | |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | Y4 | |
| +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | Y5 | |
| +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 | Y6 | |
| +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | Y7 | |
| +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | Y8 |
Вы, по-видимому, испытывали затруднения при построении столбца эффекта взаимодействия x1x2x3. Он получается перемножением всех трех столбцов и называется эффектом взаимодействия второго порядка. Эффект взаимодействия двух факторов называется эффектом взаимодействия первого порядка. Вообще эффект взаимодействия максимального порядка в полном факторном эксперименте имеет порядок, на единицу меньший числа
факторов. Довольно часто применяются синонимы: парные эффекты взаимодействия (х1x2, х2х3,...), тройные (х1х2х3, х2х3х4, ...) и т.д.
Полное число всех возможных эффектов, включая b0, линейные эффекты и взаимодействия всех порядков, равно числу опытов полного факторного эксперимента. Чтобы найти число возможных взаимодействий некоторого порядка, можно воспользоваться обычной формулой числа сочетаний:
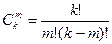 ,
,
где k – число факторов;
m – число элементов во взаимодействии. Так для плана 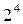 число парных взаимодействий равно шести:
число парных взаимодействий равно шести:
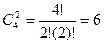 .
.
Поясним физический смысл эффекта взаимодействия следующим примером. Пусть на некоторый процесс влияют два фактора: температура и время реакции. В области низких температур увеличение времени увеличивает выход продукта. При переходе в область высоких температур эта закономерность нарушается. Здесь, напротив, необходимо уменьшать время реакции. Это и есть проявление эффекта взаимодействия.
Ортогональность матрицы планирования позволяет получить независимые друг от друга оценки коэффициентов. Это означает, что величина любого коэффициента не зависит от того, какие величины имеют другие коэффициенты. Однако сформулированные выше утверждения справедливы лишь в том случае, если модель включает только линейные эффекты и эффекты взаимодействия. Между тем существенными могут оказаться коэффициенты при квадратах факторов, их кубах и т. п. Так, для случая существенных квадратичных членов в двухфакторном эксперименте модель можно записать так:
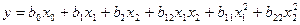 .
.
Какую информацию о квадратичных членах можно извлечь из полного факторного эксперимента? Попытка построения вектор-столбцов для 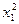 и
и 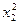 приводит к получению единичных столбцов, совпадающих друг с другом и со столбцом х0. Так как эти столбцы неразличимы, то нельзя сказать за счет чего получилась величина bо. Она включает значение свободного члена и вклады квадратичных членов. В этом случае говорят, что имеет место смешанная оценка. Это символически записывается следующим образом:
приводит к получению единичных столбцов, совпадающих друг с другом и со столбцом х0. Так как эти столбцы неразличимы, то нельзя сказать за счет чего получилась величина bо. Она включает значение свободного члена и вклады квадратичных членов. В этом случае говорят, что имеет место смешанная оценка. Это символически записывается следующим образом:
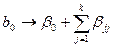 ,
,
где bo — вычисленный нами коэффициент, а греческими буквами, как принято в статистике, обозначены неизвестные истинные значения свободного члена ( 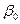 ) и квадратичных коэффициентов (
) и квадратичных коэффициентов ( 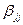 ). Если бы мы сделали сколь угодно много опытов, то в пределе получили бы истинные значения коэффициентов. На практике реализуются лишь малые выборки, по которым вычисляются оценки истинных коэффициентов.
). Если бы мы сделали сколь угодно много опытов, то в пределе получили бы истинные значения коэффициентов. На практике реализуются лишь малые выборки, по которым вычисляются оценки истинных коэффициентов.
По отношению к квадратичной модели для двух факторов получается такая система смешивания:
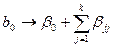 ,
, 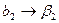 ,
, 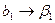 ,
, 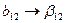 .
.
Следовательно, оценки всех коэффициентов, кроме bо, не смешаны.
Число опытов в полном факторном эксперименте превышает число коэффициентов линейной модели, причем тем больше, чем больше факторов. Разность между числом опытов и числом коэффициентов во многих случаях оказывается очень велика и возникает естественное желание сократить число необходимых опытов. Этим мы и займемся в следующем подразделе. Но прежде подведем итог сказанному.
Выводы.Первой серии опытов предшествует этап неформализованных решений, направленных на выбор локальной области факторного пространства. При этом оцениваются границы областей определения факторов, задаваемые либо принципиальными ограничениями, либо технико-экономическими соображениями, либо конкретными условиями проведения процесса. Установление области связано с тщательным анализом априорной информации об изменении параметра оптимизации и о кривизне поверхности отклика.
Локальная область проведения эксперимента выбирается в два этапа: определение основного уровня и интервалов варьирования. Основной (нулевой) уровень — многомерная точка в факторном пространстве, задаваемая комбинацией уровней факторов. Построение плана эксперимента сводится к выбору экспериментальных точек, симметричных относительно основного уровня. При установлении основного уровня приходится рассматривать различные ситуации. Ситуации задаются информацией о наилучших точках и определяют решения.
Следующий этап — выбор интервалов варьирования факторов. Для каждого фактора определяются два уровня, на которых он варьируется в эксперименте. Уровни факторов изображаются двумя точками на координатной оси, симметричными относительно основного уровня. Один из уровней — верхний, другой — нижний. Интервалом варьирования факторов называется некоторое число (свое для каждого фактора), прибавление которого к основному уровню дает верхний, а вычитание — нижний уровень. Для упрощения записи условий эксперимента и обработки экспериментальных данных масштабы по осям задают так, чтобы верхний уровень соответствовал +1, нижний —1, основной — нулю.
На выбор интервалов варьирования накладываются ограничения снизу (он не может быть меньше ошибки фиксирования уровня фактора) и сверху (верхний или нижний уровни не должны выходить за область определения). В задачах оптимизации выбирают подобласть, которая давала бы возможность реализовать шаговую процедуру движения к оптимуму. В задачах интерполяции интервал варьирования охватывает всю описываемую область.
При определении интервала варьирования используется информация о точности, с которой фиксируются значения факторов, о кривизне поверхности отклика и о диапазоне изменения параметра оптимизации. Низкая точность фиксирования факторов определяет типичное решение — широкий интервал варьирования. Для средней точности характерен выбор среднего интервала. Высокая точность обычно приводит либо к узкому интервалу, либо к среднему.
Эксперимент, в котором реализуются все возможные сочетания уровней, называется полным факторным экспериментом. Если число уровней равно двум, то это полный факторный эксперимент типа 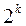 . Условия эксперимента представляют в виде таблицы — матрицы планирования, где строки соответствуют различным опытам, а столбцы — значениям факторов.
. Условия эксперимента представляют в виде таблицы — матрицы планирования, где строки соответствуют различным опытам, а столбцы — значениям факторов.
Полный факторный эксперимент типа 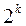 обладает свойствами симметричности, нормировки, ортогональности, ротатабельности (для линейной модели).
обладает свойствами симметричности, нормировки, ортогональности, ротатабельности (для линейной модели).
Коэффициенты, вычисленные по результатам эксперимента, указывают на силу влияния факторов. Эффект фактора численно равен удвоенному коэффициенту. В тех случаях, когда эффект одного фактора зависит от уровня, на котором находится другой фактор, говорят о наличии эффекта взаимодействия двух факторов. Для его количественной оценки получают столбец произведений этих факторов и обращаются с ним как с вектором-столбцом любого фактора.
Из полного факторного эксперимента нельзя извлечь информацию о квадратичных членах. Векторы-столбцы для квадратичных членов совпадают друг с другом "и со столбцом х0. Величина свободного члена bо включает вклады квадратичных членов, получается смешанная оценка. Оценки остальных коэффициентов не смешаны.
Если взаимное влияние факторов отсутствует или их эффектом можно пренебречь, то проводят частичный факторный эксперимент (ЧФЭ). К ним относятся [3]:
рандомизированный план;
латинский план;
классический план;
дробный факторный эксперимент.
Рандомизированный план – предполагает выбор сочетаний уровней для каждого прогона случайным образом. При использовании этого метода отправной точкой в формировании плана является число экспериментов, которые считает возможным (или необходимым) провести исследователь.
Латинский план (или «латинский квадрат») – используется в том случае, когда проводится эксперимент с одним первичным фактором и несколькими вторичными. Суть такого планирования состоит в следующем. Если первичный фактор A имеет 1 уровней, то для каждого вторичного фактора также выбирается 1 уровней. Выбор комбинации уровней факторов выполняется на основе специальной процедуры, которую мы рассмотрим на примере.
Пусть в эксперименте используется первичный фактор A и два вторичных фактора – В и C, число уровней факторов l равно 4. Соответствующий план можно представить в виде квадратной матрицы (таблица 1.10) размером l*l (4*4) относительно уровней фактора А. при этом матрица строится таким образом, чтобы в каждой строке и в каждом столбце данный уровень фактора А встречался только один раз:
Таблица 1.10 – Латинский квадрат
| Значение Фактора B | Значения фактора C | |||
| C1 | C2 | C3 | C4 | |
| B1 | A1 | A2 | A3 | A4 |
| B2 | A2 | A3 | A4 | A1 |
| B3 | A3 | A4 | A1 | A2 |
| B4 | A4 | A1 | A2 | A3 |
В результате имеет место план, требующий 4х4=16 прогонов, в отличие от ПФЭ, для которого нужно 4 ³ = 64 прогона.
Классический план – это эксперимент с изменением факторов по одному. Суть его состоит в том, что один из факторов «пробегает» все l уровней, а остальные k-1 факторов поддерживаются постоянными. Такой план обеспечивает исследование эффектов каждого фактора в отдельности. Он требует всего 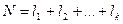 прогонов (l i– число уровней i-го фактора).
прогонов (l i– число уровней i-го фактора).
Для рассмотренного выше примера (3 фактора, по 4 уровня каждый) N=4+4+4=12. Еще раз подчеркнем, что такой план применим (как и любой ЧФЭ) только при отсутствии взаимодействия между факторами.
В полном факторном эксперименте разность между числом опытов и числом коэффициентов велика. Возникает проблема уменьшения числа опытов. Этому вопросу посвящен следующий подраздел.
Дата добавления: 2021-11-16; просмотров: 670;











